Podstawy rozwiązywania równań różniczkowych
\( \LSM{} \), metoda Galerkina i metoda kolokacji do rozwiązywania równań różniczkowych
Cel: rozwinięcie idei aproksymacji \( f \) przez \( u \), czyli rozwiązywania problemu:
$$ u = f $$
na rozwiązywanie \( \PDE \), np:
$$ -u'' + bu = f,\quad u(0)=C,\ u'(L)=D $$
Szczególny nacisk położony na metodę Galerkina.
Ogólna postać równania różniczkowego
$$
\begin{equation*}
\mathcal{L}(u) = 0,\quad x\in\Omega \end{equation*}
$$
Przykłady (dla zagadnień 1D):
$$
\begin{align*}
\mathcal{L}(u) &= \frac{d^2u}{dx^2} - f(x),\\
\mathcal{L}(u) &= \frac{d}{dx}\left(\dfc(x)\frac{du}{dx}\right) + f(x),\\
\mathcal{L}(u) &= \frac{d}{dx}\left(\dfc(u)\frac{du}{dx}\right) - au + f(x),\\
\mathcal{L}(u) &= \frac{d}{dx}\left(\dfc(u)\frac{du}{dx}\right) + f(u,x)
\end{align*}
$$
Ogólna postać warunków brzegowych
$$
\begin{equation*}
\mathcal{B}_0(u)=0,\ x=0,\quad \mathcal{B}_1(u)=0,\ x=L
\end{equation*}
$$
Przykłady:
$$
\begin{align*}
\mathcal{B}_i(u) &= u - g,\quad &\hbox{warunek Dirichleta}\\
\mathcal{B}_i(u) &= -\dfc \frac{du}{dx} - g,\quad &\hbox{warunek Neumanna}\\
\mathcal{B}_i(u) &= -\dfc \frac{du}{dx} - h(u-g),\quad &\hbox{warunek Robina}
\end{align*}
$$
Notacja - przypomnienie
- \( \uex(x) \) – rozwiązanie ścisłe (exact solution) równania \( \mathcal{L}(\uex)=0 \) + \( \mathcal{B}_i=0 \)
- \( u(x) \) – rozwiązanie przybliżone
- \( V = \hbox{span}\{ \baspsi_0(x),\ldots,\baspsi_N(x)\} \) --przestrzeń \( V \) o bazie \( \sequencei{\baspsi} \)
- Poszukiwane: \( u\in V \)
- \( \If =\{0,\ldots,N\} \) zbiór indeksów
- \( u(x) = \sum_{j\in\If} c_j\baspsi_j(x) \)
- Iloczyn skalarny: \( (u,v) = \int_\Omega uv\dx \)
- Norma: \( ||u||=\sqrt{(u,u)} \)
Sformułowanie wariacyjne i warunki brzegowe
Nowe zagadnienia:
- Sformułowanie wariacyjne równania różniczkowego
- Obchodzenie się z warunkami brzegowymi
Metoda residuów
- Rozwiązując \( u=f \) znany jest błąd \( e=f-u \) oraz zasady jego minimalizacji
- Rozwiązując \( \mathcal{L}(\uex)=f \) nie znamy \( \uex \) przez co niemożliwe jest oszacowanie błędu \( e=\uex - u \)
- Możliwe jest tylko oszacowanie błędu (nie)spełnienia równania: residuum \( R \)
Wstawiając \( u=\sum_jc_j\baspsi_j \) w \( \mathcal{L}=f \) otrzymuje się residuum \( R \).
(\( \mathcal{L}(\uex) - f = 0 \), ale \( \mathcal{L}(u) - f \neq 0 = R \))
$$
\begin{equation*}
\mathcal{L}(u) = \mathcal{L}(\sum_j c_j \baspsi_j) = R \neq 0
\end{equation*}
$$
Cel: minimalizacja \( R \) w funkcji \( \sequencei{c} \) (mamy nadzieję, że w ten sposób \( e \) również będzie mały)
$$ R=R(c_0,\ldots,c_N; x)$$
\( \LSM \)
Pomysł: minimalizacja
$$
\begin{equation*}
E = ||R||^2 = (R,R) = \int_{\Omega} R^2 dx
\end{equation*}
$$
Jeśli minimalizujemy względem \( \sequencei{c} \) to:
$$
\frac{\partial E}{\partial c_i} =
\int_{\Omega} 2R\frac{\partial R}{\partial c_i} dx = 0\quad
\Leftrightarrow\quad (R,\frac{\partial R}{\partial c_i})=0,\quad
i\in\If
$$
\( N+1 \) równań i \( N+1 \) niewiadomych \( \sequencei{c} \)
Metoda Galerkina
Pomysł: niech \( R \) będzie ortogonalne do \( V \),
$$
(R,v)=0,\quad \forall v\in V
$$
co jest równoważne
$$
(R,\baspsi_i)=0,\quad i\in\If
$$
\( N+1 \) równań i \( N+1 \) niewiadomych \( \sequencei{c} \)
Metoda residuów ważonych
- uogólnienie metody Galerkina: niech \( R \) będzie ortogonalne do pewnej przestrzeni \( W \), przy czym możliwe jest \( W\neq V \):
$$
(R,v)=0,\quad \forall v \in W
$$
Jeśli \( \{w_0,\ldots, w_N \} \) to baza dla \( W \):
$$
(R, w_i )=0,\quad i \in \If
$$
- \( N+1 \) równań i \( N+1 \) niewiadomych \( \sequencei{c} \)
- Metoda residuów z wagą \( w_i = \partial R/\partial c_i \) daje \( \LSM{} \)
Nowe pojęcia: funkcje testowe i próbne (test functions/trial functions)
- \( \baspsi_j \) wykorzystywany w \( \sum_j c_j \baspsi_j \) - funkcja próbna (f. bazowa)
- \( \baspsi_i \) lub \( w_i \) wykorzystywana jako waga w metodzie Galerkina to funkcja testowa (f. wagowa)
Metoda kolokacji
Pomysł: Niech \( R=0 \) w \( N+1 \) punktach obszaru
$$ R(\xno{i}; c_0,\ldots,c_N)=0,\quad i\in\If$$
Metoda kolokacji to metoda residuów ważonych gdzie wagi to delty Diraca
$$ 0 = \int_\Omega R(x;c_0,\ldots,c_N)
\delta(x-\xno{i})\dx = R(\xno{i}; c_0,\ldots,c_N)$$
$$
\hbox{własność } \delta(x):\quad
\int_{\Omega} f(x)\delta (x-\xno{i}) dx = f(\xno{i}),\quad \xno{i}\in\Omega
$$
Zastosowanie metod
Podanie przykładów zastosowania metod: najmniejszych kwadratów, Galerkina, kolokacji; do rozwiązywania zagadnień 1D z globalnymi funkcjami bazowymi.
Przykładowy problem
$$ -u''(x) = f(x),\quad x\in\Omega=[0,L],\quad u(0)=0,\ u(L)=0$$
Funkcje bazowe:
$$ \baspsi_i(x) = \sinL{i},\quad i\in\If$$
Residuum:
$$
\begin{align*}
R(x;c_0,\ldots,c_N) &= u''(x) + f(x),\nonumber\\
&= \frac{d^2}{dx^2}\left(\sum_{j\in\If} c_j\baspsi_j(x)\right)
+ f(x),\nonumber\\
&= -\sum_{j\in\If} c_j\baspsi_j''(x) + f(x)
\end{align*}
$$
Warunki brzegowe
Ponieważ \( u(0)=u(L)=0 \), należy zapewnić, aby dla wszystkich f-cji bazowych \( \baspsi_i(0)=\baspsi_i(L)=0 \). Jeśli tak to:
$$ u(0) = \sum_jc_j{\color{red}\baspsi_j(0)} = 0,\quad
u(L) = \sum_jc_j{\color{red}\baspsi_j(L)} =0 $$
- znane \( u \): warunek brzegowy Dirichleta
- znane \( u' \): warunek brzegowy Neumanna
- potrzebne \( \baspsi_i=0 \) spełniające warunek brzegowy Dirichleta
Metoda najmniejszych kwadratów
$$
(R,\frac{\partial R}{\partial c_i}) = 0,\quad i\in\If
$$
$$
\begin{equation*}
\frac{\partial R}{\partial c_i} =
\frac{\partial}{\partial c_i}
\left(\sum_{j\in\If} c_j\baspsi_j''(x) + f(x)\right)
= \baspsi_i''(x)
\end{equation*}
$$
Ponieważ:
\small
$$
\frac{\partial}{\partial c_i}\left(c_0\baspsi_0'' + c_1\baspsi_1'' + \cdots +
c_{i-1}\baspsi_{i-1}'' + {\color{red}c_i\baspsi_{i}''} + c_{i+1}\baspsi_{i+1}''
+ \cdots + c_N\baspsi_N'' \right) = \baspsi_{i}''
$$
Metoda najmniejszych kwadratów; URL
$$
\begin{equation*}
(\sum_j c_j \baspsi_j'' + f,\baspsi_i'')=0,\quad i\in\If
\end{equation*}
$$
Niewiadome na lewo, dane na prawo:
$$
\begin{equation*}
\sum_{j\in\If}(\baspsi_i'',\baspsi_j'')c_j = -(f,\baspsi_i''),\quad i\in\If \end{equation*}
$$
Co jest równoważne URL:
$$
\begin{equation*} \sum_{j\in\If}A_{i,j}c_j = b_i,\quad i\in\If
\end{equation*}
$$
Metoda najmniejszych kwadratów; macierz współczynników i wektor prawej strony
$$
\begin{align*}
A_{i,j} &= (\baspsi_i'',\baspsi_j'')\nonumber\\
& = \pi^4(i+1)^2(j+1)^2L^{-4}\int_0^L \sinL{i}\sinL{j}\, dx\nonumber\\
&= \left\lbrace
\begin{array}{ll} {1\over2}L^{-3}\pi^4(i+1)^4 & i=j \\ 0, & i\neq j
\end{array}\right.
\\
b_i &= -(f,\baspsi_i'') = (i+1)^2\pi^2L^{-2}\int_0^Lf(x)\sinL{i}\, dx
\end{align*}
$$
Macierz diagonalna jako wynik ortogonalności funkcji bazowych
Ortogonalność – użyteczna własność funkcji bazowych
$$
\begin{equation*}
\int\limits_0^L \sinL{i}\sinL{j}\, dx = \delta_{ij},\quad
\quad\delta_{ij} = \left\lbrace
\begin{array}{ll} \half L & i=j \\ 0, & i\neq j
\end{array}\right.
\end{equation*}
$$
\( \Rightarrow\ (\baspsi_i'',\baspsi_j'') = \delta_{ij} \),
a więc wyłącznie elementy na przekątnej \( \neq = 0 \), dzięki czemu z łatwością można znaleźć rozwiązanie:
$$
\begin{equation*}
c_i = \frac{2L}{\pi^2(i+1)^2}\int_0^Lf(x)\sinL{i}\, dx
\end{equation*}
$$
Metoda najmniejszych kwadratów; rozwiązanie
Rozwiązanie przy pomocy sympy dla \( f(x)=2 \):
from sympy import *
import sys
i, j = symbols('i j', integer=True)
x, L = symbols('x L')
f = 2
a = 2*L/(pi**2*(i+1)**2)
c_i = a*integrate(f*sin((i+1)*pi*x/L), (x, 0, L))
c_i = simplify(c_i)
print c_i
\small
$$
\begin{equation*}
c_i = 4 \frac{L^{2} \left(\left(-1\right)^{i} + 1\right)}{\pi^{3}
\left(i^{3} + 3 i^{2} + 3 i + 1\right)},\quad
u(x) = \sum_{k=0}^{N/2} \frac{8L^2}{\pi^3(2k+1)^3}\sinL{2k}
\end{equation*}
$$
\( c_i \) szybko zanikają: \( c_2 = c_0/27 \), \( c_4=c_0/125 \) - pierwszy wyraz może być całkiem niezłym przybliżeniem:
$$
\begin{equation*} u(x) \approx \frac{8L^2}{\pi^3}\sin\left(\pi\frac{x}{L}\right) \end{equation*}
$$
Metoda Galerkina
\( R=u''+f \):
$$
\begin{equation*}
(u''+f,v)=0,\quad \forall v\in V,
\end{equation*}
$$
po reorganizacji:
$$
\begin{equation*}
(u'',v) = -(f,v),\quad\forall v\in V \end{equation*}
$$
co jest sformułowaniem wariacyjnym zagadnienia opisanego \( \PDE \)
\( \forall v\in V \) jest równoważne \( \forall v\in\baspsi_i \), \( i\in\If \), i ostatecznie
$$
\begin{equation*}
(\sum_{j\in\If} c_j\baspsi_j'', \baspsi_i)=-(f,\baspsi_i),\quad i\in\If \end{equation*}
$$
$$
\begin{equation*}
\sum_{j\in\If}(\baspsi_j'', \baspsi_i) c_j=-(f,\baspsi_i),\quad i\in\If \end{equation*}
$$
Metoda Galerkina; rozwiązanie
Poniważ \( \baspsi_i''\propto -\baspsi_i \),
metoda Galerkinga daje ten sam URL i to samo rozwiązanie (w tym konkretnym przykładzie) co metoda najmniejszych kwadratów.
Metoda kolokacji
\( R=0 \) (czyli równanie różniczkowe) musi być spełnione w \( N+1 \) punktach:
$$
\begin{equation*}
-\sum_{j\in\If} c_j\baspsi_j''(\xno{i}) = f(\xno{i}),\quad i\in\If
\end{equation*}
$$
To daje URL \( \sum_j A_{i,j}=b_i \) o współczynnikach:
$$
\begin{equation*} A_{i,j}=-\baspsi_j''(\xno{i})=
(j+1)^2\pi^2L^{-2}\sin\left((j+1)\pi \frac{x_i}{L}\right),
\quad b_i=2
\end{equation*}
$$
Niech: \( N=0 \), \( x_0=L/2 \), wtedy
$$ c_0=2L^2/\pi^2 $$
Porównanie metod
- Rozwiązanie ścisłe: \( u(x)=x(L-x) \)
- m. Galerkina oraz \( \LSM{} \) (\( N=0 \)): \( u(x)=8L^2\pi^{-3}\sin (\pi x/L) \)
- m. kolokacji (\( N=0 \)): \( u(x)=2L^2\pi^{-2}\sin (\pi x/L) \).
>>> import sympy as sym
>>> # Computing with Dirichlet conditions: -u''=2 and sines
>>> x, L = sym.symbols('x L')
>>> e_Galerkin = x*(L-x) - 8*L**2*sym.pi**(-3)*sym.sin(sym.pi*x/L)
>>> e_colloc = x*(L-x) - 2*L**2*sym.pi**(-2)*sym.sin(sym.pi*x/L)
>>> # Verify max error for x=L/2
>>> dedx_Galerkin = sym.diff(e_Galerkin, x)
>>> dedx_Galerkin.subs(x, L/2)
0
>>> dedx_colloc = sym.diff(e_colloc, x)
>>> dedx_colloc.subs(x, L/2)
0
# Compute max error: x=L/2, evaluate numerical, and simplify
>>> sym.simplify(e_Galerkin.subs(x, L/2).evalf(n=3))
-0.00812*L**2
>>> sym.simplify(e_colloc.subs(x, L/2).evalf(n=3))
0.0473*L**2
Użyteczne przykłady
Zalety całkowania przez części
Od tej pory rozwiązanie równania różniczkowego będzie uzyskiwane poprzez sformułowanie słabe otrzymywane w wyniku całkowania przez części (zastosowanie tw. Greena)
$$
\begin{align*}
\int_0^L u''(x)v(x) dx &= - \int_0^Lu'(x)v'(x)dx
+ [vu']_0^L\nonumber\\
&= - \int_0^Lu'(x)v'(x) dx
+ u'(L)v(L) - u'(0)v(0)
\end{align*}
$$
Dlaczego?
- Obniżenie wymagań co do różniczkowalności
- Pozwala uzyskiwać symetryczne postaci operatorów (m.in. macierzy)
- Ułatwia implementacje warunków brzegowych Neumanna
- Standardowe funkcje bazowe na elementach skończonych \( \basphi_i \) mają nieciągłe pochodne na krańcach elementów przez co niemożliwe jest obliczenie dla nich \( \basphi_i'' \)
Sposób postępowania z niezerowym warunkiem Dirichleta
- Niech będzie dany niezerowy warunek Dirichleta, np. \( u(L)=D \)
- Żądamy \( \baspsi_i(L)=0 \) (czyli \( \baspsi_i=0 \) w punkcie występowania warunku Dirichleta)
- Problem: \( u(L) = \sum_j c_j\baspsi_j(L)=\sum_j c_j\cdot 0=0\neq D \) - zawsze!
- Rozwiązanie: \( u(x) = B(x) + \sum_j c_j\baspsi_j(x) \)
- \( B(x) \): funkcja brzegowa spełniająca warunek Dirichleta
- Jeśli \( u(L)=D \), należy dopilnować, aby \( B(L)=D \)
- Brak wymagań co do zachowania \( B(x) \) wewnątrz \( \Omega \)
Przykład stworzenia funkcji bazowej dla warunku Dirichleta z lewej i prawej strony przedziału
Warunki Dirichleta: \( u(0)=C \) and \( u(L)=D \). Niech \( B(x) \) będzie np.
$$ B(x) = \frac{1}{L}(C(L-x) + Dx):\qquad B(0)=C,\ B(L)=D $$
$$
\begin{equation*}
u(x) = B(x) + \sum_{j\in\If} c_j\baspsi_j(x),
\end{equation*}
$$
$$ u(0) = B(0)= C,\quad u(L) = B(L) = D $$
Przykład stworzenia funkcji bazowej dla jednostronnego warunku Dirichleta
Warunek Dirichleta: \( u(L)=D \). Niech \( B(x) \) będzie równe:
$$ B(x) = D:\qquad B(L)=D $$
$$
\begin{equation*}
u(x) = B(x) + \sum_{j\in\If} c_j\baspsi_j(x),
\end{equation*}
$$
$$ u(L) = B(L) = D $$
Uwzględniając \( B(x) \), \( u\not\in V \), ale \( \sum_{j}c_j\baspsi_j\in V \)
- \( \sequencei{\baspsi} \) jest bazą przestrzeni \( V \)
- \( \sum_{j\in\If}c_j\baspsi_j(x)\in V \)
- Ale \( u\not\in V \)!
- Dowód: niech \( u(0)=C \) i \( u\in V \); dla każdego \( v\in V \) jest \( v(0)=C \), ale \( 2u\not\in V \) poniważ \( 2u(0)=2C \) (zła wartość)
- Dla \( u(x) = B(x) + \sum_{j\in\If}c_j\baspsi_j(x) \), (w ogólnym przypadku) \( B\not\in V \) oraz \( u\not\in V \), ale \( (u-B)\in V \) poniważ \( \sum_{j}c_j\baspsi_j\in V \)
Notacja stosowana dla sformułowań wariacyjnych
Znaczna część literatury dot. \( \FEM{} \) stosuje specjalną notację jeśli chodzi o sformułowania wariacyjne
Znajdź takie \( (u-B)\in V \), że
$$ a(u,v) = L(v)\quad \forall v\in V $$
Przykład zastosowania notacji
$$ -u''=f, \quad u'(0)=C,\ u(L)=D,\quad u=D + \sum_jc_j\baspsi_j$$
Sformułowanie wariacyjne (słabe):
$$
\int_{\Omega} u' v'dx = \int_{\Omega} fvdx - v(0)C
\quad\hbox{or}\quad (u',v') = (f,v) - v(0)C
\quad\forall v\in V
$$
W zaproponowanej abstrakcyjnej notacji: znajdź \( (u-B)\in V \) takie, że
$$ a(u,v) = L(v)\quad \forall v\in V$$
a więc
$$ a(u,v) = (u',v'),\quad L(v) = (f,v) -v(0)C $$
Formy dwuliniowe i liniowe
- \( a(u,v) \) jest formą dwuliniową
- \( L(v) \) jest formą liniową
Dla form liniowych
$$ L(\alpha_1 v_1 + \alpha_2 v_2)
=\alpha_1 L(v_1) + \alpha_2 L(v_2),
$$
Dla form dwuliniowych
$$
\begin{align*}
a(\alpha_1 u_1 + \alpha_2 u_2, v) &= \alpha_1 a(u_1,v) + \alpha_2 a(u_2, v),
\\
a(u, \alpha_1 v_1 + \alpha_2 v_2) &= \alpha_1 a(u,v_1) + \alpha_2 a(u, v_2)
\end{align*}
$$
W zagadnieniach nieliniowych: Znależć \( (u-B)\in V \) takie, że \( F(u;v)=0\ \forall v\in V \)
URL związany z równaniem wyrażonym w notacji abstrakcyjnej
$$ a(u,v) = L(v)\quad \forall v\in V\quad\Leftrightarrow\quad
a(u,\baspsi_i) = L(\baspsi_i)\quad i\in\If$$
URL odpowiadający powyższemu równaniu można otrzymać wstawiając do niego \( u = B + \sum_jc_j\baspsi_j \):
$$ a(B + \sum_{j\in\If} c_j \baspsi_j,\baspsi_i)c_j = L(\baspsi_i)\quad i\in\If$$
Ze wzgledu na liniowość,
$$ \sum_{j\in\If} \underbrace{a(\baspsi_j,\baspsi_i)}_{A_{i,j}}c_j =
\underbrace{L(\baspsi_i) - a(B,\baspsi_i)}_{b_i}\quad i\in\If$$
Równoważność sformułowań wariacyjnych i metod energetycznych
Jeśli \( a \) jest symetryczne: \( a(u,v)=a(v,u) \), wtedy
$$ a(u,v)=L(v)\quad\forall v\in V$$
jest równoważne minimalizacji funkcjonału
$$ F(v) = {\half}a(v,v) - L(v) $$
dla wszystkich \( v\in V \). Czyli
$$ F(u)\leq F(v)\quad \forall v\in V $$
- Sformułowanie często stosowane w początkach rozwoju \( \FEM{} \)
- Wciąż stosowane w zagadnieniach sprężystości i analizy dynamicznej struktur mechanicznych
- Podejście nie tak ogólne jak m. Galerkina (ze względu na wymóg symetryczności \( a(u,v)=a(v,u) \))
Przykłady sformułowań wariacyjnych
Wyprowadzić sformułowania wariacyjne dla pewnych typów równań różniczkowych w 1D uwzględniających
- zmienne współczynniki
- mieszane warunki brzegowe typu Dirichleta i Neumanna
- współczynniki nieliniowe
Problem 1: uwzględnienie zmiennego współczynnika
$$
\begin{equation*}
-\frac{d}{dx}\left( \dfc(x)\frac{du}{dx}\right) = f(x),\quad x\in\Omega =[0,L],\
u(0)=C,\ u(L)=D
\end{equation*}
$$
- współczynnik \( \dfc(x) \) zależny od zmiennej \( x \)
- \( V = \hbox{span}\{\baspsi_0,\ldots,\baspsi_N\} \)
- Niezerowy warunek Dirichleta w \( x=0 \) oraz \( x=L \)
- Z kolei \( \baspsi_i(0)=\baspsi_i(L)=0 \)
- a więc dla każdego \( v\in V \) będzie \( v(0)=v(L)=0 \)
- Rozwiązanie problemu -> niech: \( B(x) = C + \frac{1}{L}(D-C)x \), wtedy
$$
u(x) = B(x) + \sum_{j\in\If} c_j\baspsi_i(x),\quad
$$
Problem 1: uwzględnienie zmiennego współczynnika – m. Galerkina
$$ R = -\frac{d}{dx}\left( a\frac{du}{dx}\right) -f $$
co zapisane w postaci wariacyjnej:
$$
(R, v) = 0,\quad \forall v\in V
$$
lub jawnie:
$$
\int_{\Omega} \left(-\frac{d}{dx}\left( \dfc\frac{du}{dx}\right) -f\right)v \dx = 0,\quad \forall v\in V
$$
Problem 1: uwzględnienie zmiennego współczynnika – całkowanie przez części
$$ -\int_{\Omega} \frac{d}{dx}\left( \dfc(x)\frac{du}{dx}\right) v \dx
= \int_{\Omega} \dfc(x)\frac{du}{dx}\frac{dv}{dx}\dx -
\left[\dfc\frac{du}{dx}v\right]_0^L
$$
Ostatni wyraz prawej strony znika ponieważ \( v(0)=v(L)=0 \)
Problem 1: uwzględnienie zmiennego współczynnika – sformułowanie wariacyjne
Znaleźć \( (u-B)\in V \) takie, że
$$
\int_{\Omega} \dfc(x)\frac{du}{dx}\frac{dv}{dx}dx = \int_{\Omega} f(x)vdx,\quad
\forall v\in V
$$
Po zastosowaniu zwięzłej notacji:
$$ \underbrace{(\dfc u',v')}_{a(u,v)} = \underbrace{(f,v)}_{L(v)},
\quad \forall v\in V $$
Problem 1: uwzględnienie zmiennego współczynnika – URL 1
Uwzględniając
$$ a(u,v) = (\dfc u', v'),\quad L(v) = (f,v) $$
można wygenerować URL gdzie:
$$
\begin{align*}
A_{i,j} &= a(\baspsi_j,\baspsi_i) = (\dfc \baspsi_j', \baspsi_i')
= \int_\Omega \dfc \baspsi_j' \baspsi_i'\dx =
\int_\Omega \baspsi_i' \dfc \baspsi_j'\dx = \\
& = a(\baspsi_i,\baspsi_j) = A_{j,i}\\
b_i &= (f,\baspsi_i) - (\dfc B',\baspsi_i) = \int_\Omega (f\baspsi_i -
\dfc L^{-1}(D-C)\baspsi_i')\dx
\end{align*}
$$
Uwzględnienie zmiennego współczynnika; pełne wyprowadzenie URL
\( v=\baspsi_i \) oraz \( u=B + \sum_jc_j\baspsi_j \):
$$
(\dfc B' + \dfc \sum_{j\in\If} c_j \baspsi_j', \baspsi_i') =
(f,\baspsi_i), \quad i\in\If
$$
Porządkując składniki otrzymuje się
$$ \sum_{j\in\If} (\dfc\baspsi_j', \baspsi_i')c_j =
(f,\baspsi_i) + (aL^{-1}(D-C), \baspsi_i'), \quad i\in\If
$$
czyli URL dany przez \( \sum_j A_{i,j}c_j=b_i \) gdzie
$$
\begin{align*}
A_{i,j} &= (a\baspsi_j', \baspsi_i') = \int_{\Omega} \dfc(x)\baspsi_j'(x)
\baspsi_i'(x)\dx\\
b_i &= (f,\baspsi_i) + (aL^{-1}(D-C),\baspsi_i')=
\int_{\Omega} \left(f\baspsi_i + \dfc\frac{D-C}{L}\baspsi_i'\right) \dx
\end{align*}
$$
Uwzględnienie funkcji pochodnej w równaniu i warunku brzegowym
$$
-u''(x) + bu'(x) = f(x),\quad x\in\Omega =[0,L],\
u(0)=C,\ u'(L)=E
$$
Nowy problem:
- pochodna pierwszego rzędu \( u' \) w równaniu
- warunek brzegowy – wymuszona wartość pochodnej rozwiązania \( u' \): \( u'(L)=E \)
Jak postępować?:
- Zakładamy \( \baspsi_i(0)=0 \) ze względu na warunek Dirichleta w \( x=0 \)
- Wybieramy: \( B(x)=C(L-x) \) lub po prostu \( B(x)=C \)
- Brak wymagań co do wartości \( \baspsi_i(L) \) (bo brak war. Dir. w \( x=L \))
Uwzględnienie funkcji pochodnej w równaniu i warunku brzegowym, szczegóły
$$ u = C + \sum_{j\in\If} c_j \baspsi_i(x)$$
Metoda Galerkina: mnożymy przez funkcję wagową \( v \), całkujemy nad \( \Omega \), całkujemy przez części:
$$ (-u'' + bu' - f, v) = 0,\quad\forall v\in V$$
$$ (u',v') + (bu',v) = (f,v) + [u' v]_0^L, \quad\forall v\in V$$
\( [u' v]_0^L = u'(L)v(L) - u'(0)v(0)= E v(L) \) ponieważ \( v(0)=0 \) a \( u'(L)=E \)
$$ (u',v') + (bu',v) = (f,v) + Ev(L), \quad\forall v\in V$$
Uwzględnienie funkcji pochodnej w równaniu i warunku brzegowym, spostrzeżenia
$$ (u',v') + (bu',v) = (f,v) + Ev(L), \quad\forall v\in V$$
Ważne spotrzeżenia:
- Współczynnik wynikający z całkowania przez części, a dotyczący całki po brzegu (\( [u' v]_0^L \)) może zostać użyty do implementacji warunku Neumanna
- Nie uwgzlędnienie tego współczynnika jest równoznaczne z wymuszaniem warunku \( u'=0 \) (!)
- Tego rodzaju warunek brzegowy nazywany jest naturalnym warunkiem brzegowym (warunek brzegowy spełniany jest w sposób naturalny)
Uwzględnienie funkcji pochodnej w równaniu i warunku brzegowym, notacja uogólniona
Uogólniony zapis problemu:
$$ a(u,v)=L(v)\quad\forall v\in V$$
gdzie dla
$$ (u',v') + (bu',v) = (f,v) + Ev(L), \quad\forall v\in V$$
mamy
$$
\begin{align*}
a(u,v)&=(u',v') + (bu',v)\\
L(v)&= (f,v) + E v(L)
\end{align*}
$$
Uwzględnienie funkcji pochodnej w równaniu i warunku brzegowym, URL
Wstawiając \( u=C+\sum_jc_j\baspsi_j \) oraz \( v=\baspsi_i \) do
$$ (u',v') + (bu',v) = (f,v) + Ev(L), \quad\forall v\in V$$
można otrzymać
$$
\sum_{j\in\If}
\underbrace{((\baspsi_j',\baspsi_i') + (b\baspsi_j',\baspsi_i))}_{A_{i,j}}
c_j =
\underbrace{(f,\baspsi_i) + E \baspsi_i(L)}_{b_i},\quad i\in\If
$$
Spostrzeżenie: \( A_{i,j} \) tym razem nie jest symetryczna, ze względu na istnienie wyrazu
$$
(b\baspsi_j',\baspsi_i)=\int_{\Omega} b\baspsi_j'\baspsi_i dx
\neq \int_{\Omega} b \baspsi_i' \baspsi_jdx = (\baspsi_i',b\baspsi_j)
$$
Nazewnictwo: warunki brzegowe naturalne i podstawowe
$$ (u',v') + (bu',v) = (f,v) + u'(L)v(L) - u'(0)v(0)$$
- Przypomnienie: zapomnienie o uwzględnieniu warunku brzegowego równoważne \( u'(L)=u'(0)=0 \) (chyba, że wymuszono war. Dirichleta)
- Wymóg wartości pochodnej funkcji \( u' \) jest nazywamy warunkiem naturalnym (ang. natural condition) i jest uwzględnianiy w równaniu poprzez zwykłe ''wstawienie'' wartości do równania w postaci wariacyjne
- Wymóg wartości funkcji \( u \) na brzegu wymaga modyfikacji \( V \) (\( \baspsi_i(0)=0 \) lub/i odpowiednio \( \baspsi_i(L)=0 \) ) i jest nazywany warunkiem podstawowym (ang. essential boundary condition)
Łatwo zapomnieć o uwzględnieniu warunku brzegowego całkując przez części. W ten sposób pomyłkowo przypisujemy warunek \( u'=0 \) na danej części brzegu!
Uwzględnienie nieliniowego współczynnika
Problem:
$$
\begin{equation*}
-(\dfc(u)u')' = f(u),\quad x\in [0,L],\ u(0)=0,\ u'(L)=E
\end{equation*}
$$
- \( V \) to baza \( \sequencei{\baspsi} \) z \( \baspsi_i(0)=0 \) ze względu na \( u(0)=0 \)
- Jak bardzo nieliniowe współczynniki \( \dfc(u) \) oraz \( f(u) \) wpływają na sformułowanie wariacyjne? (Nie bardzo!)
Uwzględnienie nieliniowego współczynnika, sformułowanie wariacyjne
m. Gal.: przemnóż przez \( v \), scałkuj, scałkuj przez części
$$ \int_0^L \dfc(u)\frac{du}{dx}\frac{dv}{dx}\dx =
\int_0^L f(u)v\dx + [\dfc(u)vu']_0^L\quad\forall v\in V
$$
- \( \dfc(u(0))v(0)u'(0)=0 \) ponieważ \( v(0) \)
- \( \dfc(u(L))v(L)u'(L) = \dfc(u(L))v(L)E \) ponieważ \( u'(L)=E \)
$$ \int_0^L \dfc(u)\frac{du}{dx}\frac{dv}{dx}v\dx =
\int_0^L f(u)v\dx + \dfc(u(L))v(L)E\quad\forall v\in V
$$
lub
$$ (\dfc(u)u', v') = (f(u),v) + \dfc(u(L))v(L)E\quad\forall v\in V
$$
Uwzględnienie nieliniowego współczynnika, kłopoty spowodowane przez nieliniowość
- Brak możliwości użycia \( a(u,v) \) oraz \( L(v) \) w abstrakcyjnym zapisie równania, ponieważ \( a \) oraz \( L \) stają się nieliniowe
- Abstrakcyjny opis w najbardziej ogólnej postaci: \( F(u;v)=0\ \forall v\in V \)
- Co z URL? -> Otrzymujemy nieliniowy układ równań algebraicznych
- Aby go rozwiązać musimy skorzystać z iteracji Picarda lub metody Newtona rozwiązywania układów równań nieliniowych
- Mimo wszystko: sformułowanie wariacyjne niezbyt the variational formulation was not much affected by nonlinearities
Przykłady obliczeń ręcznych
Uwzględnienie warunków Dirichleta i Neumanna
$$
\begin{equation*}
-u''(x)=f(x),\quad x\in \Omega=[0,1],\quad u'(0)=C,\ u(1)=D
\end{equation*}
$$
- Niech dana będzie baza wielomianów w postaci potęgowej \( \baspsi_i\sim x^i \) na \( [0,1] \)
- Ponieważ \( u(1)=D \): \( \baspsi_i(1)=0 \)
- Modyfikacja bazy: \( \baspsi_i(x)=(1-x)^{i+1},\quad i\in\If \)
- Funkcja uwzględniająca war. brzeg.: \( B(x)=Dx \)
- \( u(x) = B(x) + \sum_{j\in\If}c_j\baspsi_j = Dx + \sum_{j\in\If} c_j(1-x)^{j+1} \)
Sformułowanie wariacyjne: znaleźć \( (u-B)\in V \) takie, aby
$$
(u',\baspsi_i') = (f,\baspsi_i) - C\baspsi_i(0),\ i\in\If
$$
Uwzględnienie warunków Dirichleta i Neumanna; URL
Uwzględniając \( u(x) = B(x) + \sum_{j\in\If}c_j\baspsi_j \) otrzymuje się
$$ \sum_{j\in\If} A_{i,j}c_j = b_i,\quad i\in\If$$
gdzie
$$ A_{i,j} = (\baspsi_j',\baspsi_i')
$$
$$ b_i = (f,\baspsi_i) - (D,\baspsi_i') -C\baspsi_i(0) $$
Uwzględnienie warunków Dirichleta i Neumanna; całkowanie
$$ A_{i,j} = (\baspsi_j',\baspsi_i') = \int_{0}^1 \baspsi_i'(x)\baspsi_j'(x)dx
= \int_0^1 (i+1)(j+1)(1-x)^{i+j} dx
$$
Wybierzmy \( f(x)=2 \):
$$
\begin{align*}
b_i &= (2,\baspsi_i) - (D,\baspsi_i') -C\baspsi_i(0)\\
&= \int_0^1 \left( 2(1-x)^{i+1} - D(i+1)(1-x)^i\right)dx -C\baspsi_i(0)
\end{align*}
$$
Uwzględnienie warunków Dirichleta i Neumanna; URL \( 2\times 2 \)
Łatwość obliczeń z wykorzystaniem sympy. \( N=1 \) oraz \( \If = \{0,1\} \):
$$
\begin{equation*}
\left(\begin{array}{cc}
1 & 1\\
1 & 4/3
\end{array}\right)
\left(\begin{array}{c}
c_0\\
c_1
\end{array}\right)
=
\left(\begin{array}{c}
-C+D+1\\
2/3 -C + D
\end{array}\right)
\end{equation*}
$$
$$ c_0=-C+D+2, \quad c_1=-1,$$
$$ u(x) = 1 -x^2 + D + C(x-1)\quad\hbox{(ścisłe rozwiązanie)} $$
Kiedy rozwiązanie numeryczne jest dokładne?
Niech, poza warunkami brzegowymi Dirichleta, \( \uex \) leży w przestrzeni \( V \), w której poszukiwane jest \( u \) (\( u_e - B \in V \)). Wtedy:
$$
\begin{align*}
u &= B + {\color{red}F},\quad F\in V\\
a(B+F, v) &= L(v),\quad\forall v\in V\\
\uex & = B + {\color{red}E},\quad E\in V\\
a(B+E, v) &= L(v),\quad\forall v\in V
\end{align*}
$$
Odejmując od siebie równania otrzymuje się: \( a(F-E,v)=0 \)
z czego wynika, że:
\( E=F \) oraz \( u = \uex \)
Obliczenia przy pomocy elementów skończonych
Problem :
- Rozwiązać problem dany równaniem \( -u''(x)=2 \), \( u(0)=u(L)=0 \)
- Wykorzystać siatkę jednorodnych elementów skończonych typu P1
- Przedstawić szczegóły wszystkich etapów obliczeń
Sformułowanie wariacyjne
Problem w postaci klasycznej:
$$ -u''(x) = 2,\quad x\in (0,L),\ u(0)=u(L)=0,$$
Sformułowanie wariacyjne:
$$ (u',v') = (2,v)\quad\forall v\in V $$
Sposób postępowania z warunkami brzegowymi
Ponieważ \( u(0)=0 \) oraz \( u(L)=0 \) należy wymusić
$$ v(0)=v(L)=0,\quad \baspsi_i(0)=\baspsi_i(L)=0$$
Wybieramy jako funkcje bazowe funkcje trójkątne: \( \baspsi_i=\basphi_i \), \( i=0,\ldots,N_n-1 \).
Problem: funkcje skrajne nie spełniają warunków brzegowych \( \basphi_0(0)\neq 0 \) oraz \( \basphi_{N_n-1}(L)\neq 0 \)
Rozwiązanie: wykluczamy z bazy \( \basphi_0 \) oraz \( \basphi_{N_n-1} \) i pracujemy na tak okrojonej bazie:
$$ \baspsi_i=\basphi_{i+1},\quad i=0,\ldots,N=N_n-3$$
Wprowadzając stosowną indeksacje \( \nu(i) \): \( \baspsi_i = \basphi_{\nu(i)} \) otrzymuje się:
$$ u = \sum_{j\in\If}c_j\basphi_{\nu(j)},\quad i=0,\ldots,N,\quad \nu(j) = j+1$$
W przypadku numeracji nieregularnej: tablica \( \nu(j) \) będzie bardziej skomplikowana
Obliczenia we współrzędnych globalnych; wzory
$$
\begin{equation*}
A_{i,j}=\int_0^L\basphi_{i+1}'(x)\basphi_{j+1}'(x) dx,\quad
b_i=\int_0^L2\basphi_{i+1}(x) dx
\end{equation*}
$$
Wygodnie jest przeprowadzić reindeksację:
\( i+1\rightarrow i \), \( j+1\rightarrow j \)aby otrzymać wzory: \( \basphi_i'\basphi_j' \), zamiast \( \basphi'_{i+1} \basphi'_{j+1} \)
$$
\begin{equation*}
A_{i-1,j-1}=\int_0^L\basphi_{i}'(x)\basphi_{j}'(x) \dx,\quad
b_{i-1}=\int_0^L2\basphi_{i}(x) \dx
\end{equation*}
$$
Obliczenia we współrzędnych globalnych; szczegóły
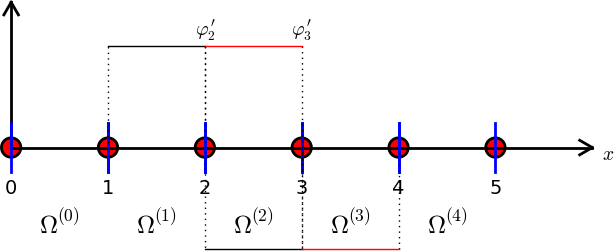
$$ \basphi_i' \sim \pm h^{-1} $$
$$ A_{i-1,i-1} = h^{-2}2h = 2h^{-1},\quad
A_{i-1,i-2} = h^{-1}(-h^{-1})h = -h^{-1}$$
oraz \( A_{i-1,i}=A_{i-1,i-2} \)
$$ b_{i-1} = 2({\half}h + {\half}h) = 2h$$
Obliczenia we współrzędnych globalnych; URL
$$
\begin{equation*}
\frac{1}{h}\left(
\begin{array}{ccccccccc}
2 & -1 & 0
&\cdots &
\cdots & \cdots & \cdots &
\cdots & 0 \\
-1 & 2 & -1 & \ddots & & & & & \vdots \\
0 & -1 & 2 & -1 &
\ddots & & & & \vdots \\
\vdots & \ddots & & \ddots & \ddots & 0 & & & \vdots \\
\vdots & & \ddots & \ddots & \ddots & \ddots & \ddots & & \vdots \\
\vdots & & & 0 & -1 & 2 & -1 & \ddots & \vdots \\
\vdots & & & & \ddots & \ddots & \ddots &\ddots & 0 \\
\vdots & & & & &\ddots & \ddots &\ddots & -1 \\
0 &\cdots & \cdots &\cdots & \cdots & \cdots & 0 & -1 & 2
\end{array}
\right)
\left(
\begin{array}{c}
c_0 \\
\vdots\\
\vdots\\
\vdots \\
\vdots \\
\vdots \\
\vdots \\
\vdots\\
c_{N}
\end{array}
\right)
=
\left(
\begin{array}{c}
2h \\
\vdots\\
\vdots\\
\vdots \\
\vdots \\
\vdots \\
\vdots \\
\vdots\\
2h
\end{array}
\right)
\end{equation*}
$$
Równanie różnicowe odpowiadające pojedyńczemu równaniu \( \FEM{} \)
Równanie dla \( i \). węzła:
$$
-\frac{1}{h}c_{i-1} + \frac{2}{h}c_{i} - \frac{1}{h}c_{i+1} = 2h
$$
Ponieważ, \( c_i = u(\xno{i+1})\equiv u_{i+1} \), równanie dla \( i-1 \). węzła ma postać:
$$
-\frac{1}{h}c_{i-2} + \frac{2}{h}c_{i-1} - \frac{1}{h}c_{i} = 2h
$$
i jest równoważne
$$
-\frac{1}{h}u_{i-1} + \frac{2}{h}u_{i} - \frac{1}{h}u_{i+1} = 2h
$$
Porównanie \( \FEM \) i \( \FDM \)
Równanie \( \FDM{} \) dla problemu \( -u''=2 \) ma postać
$$ -\frac{1}{h^2}u_{i-1} + \frac{2}{h^2}u_{i} - \frac{1}{h^2}u_{i+1} = 2 $$
Po pomnożeniu przez \( h \) okazuje się, że:
\( \FEM \) i \( \FDM \) dają równoważne URL w tym zagadnieniu.
(Równania dla węzłów brzegowych również są w tym przypadku identyczne)
Obliczenia we współrzędnych lokalnych; wzory
- Powtórz obliczenia z poprzedniego przykładu, tym razem wykonując obliczenia z perspektywy komórek.
- Obliczenia wykonuj komórka po komórce
- Każde obliczenia wykonuj wykonując transformację współrzędnych globalnych do współrzędnych unormowanych \( X\in [-1,1] \)
$$
\begin{equation*}
A_{i-1,j-1}^{(e)}=\int_{\Omega^{(e)}} \basphi_i'(x)\basphi_j'(x) \dx
= \int_{-1}^1 \frac{d}{dx}\refphi_r(X)\frac{d}{dx}\refphi_s(X)
\frac{h}{2} \dX,
\end{equation*}
$$
$$ \refphi_0(X)=\half(1-X),\quad\refphi_1(X)=\half(1+X)$$
$$ \frac{d\refphi_0}{dX} = -\half,\quad \frac{d\refphi_1}{dX} = \half $$
Z reguły łańcuchowej:
$$ \frac{d\refphi_r}{dx} = \frac{d\refphi_r}{dX}\frac{dX}{dx}
= \frac{2}{h}\frac{d\refphi_r}{dX}$$
Obliczenia we współrzędnych lokalnych; szczegóły
$$
\begin{equation*}
A_{i-1,j-1}^{(e)}=\int_{\Omega^{(e)}} \basphi_i'(x)\basphi_j'(x) \dx
= \int_{-1}^1 \frac{2}{h}\frac{d\refphi_r}{dX}\frac{2}{h}\frac{d\refphi_s}{dX}
\frac{h}{2} \dX = \tilde A_{r,s}^{(e)}
\end{equation*}
$$
$$
\begin{equation*}
b_{i-1}^{(e)} = \int_{\Omega^{(e)}} 2\basphi_i(x) \dx =
\int_{-1}^12\refphi_r(X)\frac{h}{2} \dX = \tilde b_{r}^{(e)},
\quad i=q(e,r),\ r=0,1
\end{equation*}
$$
Obliczenia należy wykonać dla indeksów \( r,s \) przyjmujących wszystkie możliwe kombinacje wartości \( 0,1 \), obliczając za każdym razem jeden z elementów lokalnej macierzy oraz wektora:
$$
\begin{equation*}
\tilde A^{(e)} =\frac{1}{h}\left(\begin{array}{rr}
1 & -1\\
-1 & 1
\end{array}\right),\quad
\tilde b^{(e)} = h\left(\begin{array}{c}
1\\
1
\end{array}\right)
\end{equation*}
$$
Przykład:
$$ \tilde A^{(e)}_{0,1} =
\int_{-1}^1 \frac{2}{h}\frac{d\refphi_0}{dX}\frac{2}{h}\frac{d\refphi_1}{dX}
\frac{h}{2} \dX
= \frac{2}{h}(-\half)\frac{2}{h}\half\frac{h}{2} \int_{-1}^1\dX
= -\frac{1}{h}
$$
Obliczenia we współrzędnych lokalnych; szczegóły
- Elementy skrajne zawierają jedynie jedną niewiadomą
- \( \Omega^{(0)} \): wartość w lewym węźle znana, przyczynek tylko od prawego węzła
- \( \Omega^{(N_e)} \): wartość w prawym węźle znana, przyczynek tylko od lewego węzła
Dla \( e=0 \) oraz \( e=N_e \):
$$
\tilde A^{(e)} =\frac{1}{h}\left(\begin{array}{r}
1
\end{array}\right),\quad
\tilde b^{(e)} = h\left(\begin{array}{c}
1
\end{array}\right)
$$
Jeden stopień swobody ("węzeł") w skrajnych elementach (\( r=0 \) odpowiada jednemu stopniowi swobody)
Obliczenia we współrzędnych lokalnych; assembling
4 elementy typu P1:
vertices = [0, 0.5, 1, 1.5, 2]
cells = [[0, 1], [1, 2], [2, 3], [3, 4]]
dof_map = [[0], [0, 1], [1, 2], [2]] # only 1 dof in elm 0, 3
Kod Pythona wykonujący assembling macierzy globalnej:
# Ae[e][r,s]: element matrix, be[e][r]: element vector
# A[i,j]: coefficient matrix, b[i]: right-hand side
for e in range(len(Ae)):
for r in range(Ae[e].shape[0]):
for s in range(Ae[e].shape[1]):
A[dof_map[e,r],dof_map[e,s]] += Ae[e][i,j]
b[dof_map[e,r]] += be[e][i,j]
W wyniku powstaje ten sam URL co w przypadku obliczeń we współrzędnych globalnych.
Uniwersalna metoda konstrukcji funkcji spełniających warunki brzegowe - warunek Dirichleta
- Stworzenie funkcji \( B(x) \) czasem bywa niełatwe w szczególności dla problemów 2D oraz 3D
- Przy pomocy funkcji bazowych \( \basphi_i \), można jednak podać uniwersalny i ogólny sposób jej konstrukcji (!)
Niech
- \( \Ifb \): zbiór indeksów z węzłami gdzie \( u \) jest znane
- \( U_i \): wartości funkcji wynikająca z warunku Dirichleta w węźle \( i \)., \( i\in\Ifb \)
Ogólna postać funkcji \( B \):
$$
\begin{equation*}
B(x) = \sum_{j\in\Ifb} U_j\basphi_j(x)
\end{equation*}
$$
Wyjaśnienie
Niech dany będzie warunek Dirichleta \( u(\xno{k})=U_k \), \( k\in\Ifb \):
$$
u(\xno{k}) = \sum_{j\in\Ifb} U_j\underbrace{\basphi_j(x)}_{\neq 0
\hbox{ tylko dla }j=k} +
\sum_{j\in\If} c_j\underbrace{\basphi_{\nu(j)}(\xno{k})}_{=0,\ k\not\in\If}
= U_k $$
Przykład: zagadnienie brzegowe z dwoma niejednorodnymi warunkami Dirichleta; sformułowanie wariacyjne
$$ -u''=2, \quad u(0)=C,\ u(L)=D $$
$$ \int_0^L u'v'\dx = \int_0^L2v\dx\quad\forall v\in V$$
$$ (u',v') = (2,v)\quad\forall v\in V$$
Przykład: zagadnienie brzegowe z dwoma niejednorodnymi warunkami Dirichleta; funkcja \( B \)
$$
\begin{equation*}
B(x) = \sum_{j\in\Ifb} U_j\basphi_j(x)
\end{equation*}
$$
W tym wypadku \( \Ifb = \{0,N_n-1\} \), \( U_0=C \), \( U_{N_n-1}=D \); \( \baspsi_i \) są funkcjami związanymi z węzłami wewnątrz obszaru \( \basphi_i \):
$$ \baspsi_i = \basphi_{\nu(i)}, \quad \nu(i)=i+1,\quad i\in\If =
\{0,\ldots,N=N_n-3\} $$
$$
\begin{align*}
u(x) &= \underbrace{C\cdot\basphi_0 + D\basphi_{N_n-1}}_{B(x)}
+ \sum_{j\in\If} c_j\basphi_{j+1}\\
&= C\cdot\basphi_0 + D\basphi_{N_n-1} + c_0\basphi_1 + c_1\basphi_2 +\cdots
+ c_N\basphi_{N_n-2}
\end{align*}
$$
Przykład: zagadnienie brzegowe z dwoma niejednorodnymi warunkami Dirichleta; szczegóły
Wstawmy \( u = B + \sum_j c_j\baspsi_j \) do sformułowania wariacyjnego:
$$ (u',v') = (2,v)\quad\Rightarrow\quad (\sum_jc_j\baspsi_j',\baspsi_i')
= (2-B',\baspsi_i)\quad \forall v\in V$$
$$
\begin{align*}
A_{i-1,j-1} &= \int_0^L \basphi_i'(x)\basphi_j'(x) \dx\\
b_{i-1} &= \int_0^L (f(x)\basphi_i(x) -
B'(x)\basphi_i'(x))\dx,\quad B'(x)=C\basphi_{0}'(x) + D\basphi_{N_n-1}'(x)
\end{align*}
$$
for \( i,j = 1,\ldots,N+1=N_n-1 \).
Przyczynki pochodzące od warunków brzegowych - od całki \( -\int B'\basphi_i'\dx \): \( C/h \) należy dodać do \( b_0 \), \( D/h \) należy dodać do \( b_N \).
Przykład: zagadnienie brzegowe z dwoma niejednorodnymi warunkami Dirichleta; obliczenia we wsp. lokalnych
- Obliczenia macierzy lokalnych - jak w poprzednim przykładzie
- Nowa postać lokalnych wektorów prawej strony - dla pierwszego i ostatniego elementu
\footnotesize
Dla pierwszego elementu:
$$
\begin{align*}
\tilde b_0^{(1)} = \int_{-1}^1 \left(f\refphi_1 -
C\frac{2}{h}\frac{d\refphi_0}{dX}\frac{2}{h}\frac{d\refphi_1}{dX}\right)
\frac{h}{2} \dX = \\
\frac{h}{2} 2\int_{-1}^1 \refphi_1 \dX
- C\frac{2}{h}(-\frac{1}{2})\frac{2}{h}\frac{1}{2}\frac{h}{2}\cdot 2
= h + C\frac{1}{h}\tp
\end{align*}
$$
Dla ostatniego elementu:
$$
\begin{align*}
\tilde b_0^{N_e} = \int_{-1}^1 \left(f\refphi_0 -
D\frac{2}{h}\frac{d\refphi_1}{dX}\frac{2}{h}\frac{d\refphi_0}{dX}\right)
\frac{h}{2} \dX = \\
\frac{h}{2} 2\int_{-1}^1 \refphi_0 \dX
- D\frac{2}{h}\frac{1}{2}\frac{2}{h}(-\frac{1}{2})\frac{h}{2}\cdot 2
= h + D\frac{1}{h}\tp
\end{align*}
$$
Sposoby modyfikacji URL
- Metoda 1: uwzględnij wartości war. Dir. poprzez funkcję \( B(x) \) i zażądaj \( \baspsi_i=0 \) na brzegu Dirichleta
- Metoda 2: zrezygnuj z \( B(x) \), zrezygnuj z warunków na \( \baspsi_i \), wygeneruj URL tak jakby warunku Dirichleta nie było i dopiero wykonaj stosowne modyfikacje bezpośrednio na URL
Metoda 2: zawsze wybieraj \( \baspsi_i = \basphi_i \) dla wszystkich \( i\in\If \):
$$
\begin{equation*}
u(x) = \sum_{j\in\If}c_j\basphi_j(x),\quad \If=\{0,\ldots,N=N_n-1\}
\end{equation*}
$$
Wszystkie Wartości \( u \) (również te na brzegu Dirichleta) można traktować jako niewiadome (wymagające obliczenia).
Modyfikacja URL; układ w postaci oryginalnej
$$ -u''=2,\quad u(0)=0,\ u(L)=D$$
Macierz w postaci identycznej jakby warunku Dirichleta nie było:
$$
\begin{equation*}
\frac{1}{h}\left(
\begin{array}{ccccccccc}
1 & -1 & 0
&\cdots &
\cdots & \cdots & \cdots &
\cdots & 0 \\
-1 & 2 & -1 & \ddots & & & & & \vdots \\
0 & -1 & 2 & -1 &
\ddots & & & & \vdots \\
\vdots & \ddots & & \ddots & \ddots & 0 & & & \vdots \\
\vdots & & \ddots & \ddots & \ddots & \ddots & \ddots & & \vdots \\
\vdots & & & 0 & -1 & 2 & -1 & \ddots & \vdots \\
\vdots & & & & \ddots & \ddots & \ddots &\ddots & 0 \\
\vdots & & & & &\ddots & \ddots &\ddots & -1 \\
0 &\cdots & \cdots &\cdots & \cdots & \cdots & 0 & -1 & 1
\end{array}
\right)
\left(
\begin{array}{c}
c_0 \\
\vdots\\
\vdots\\
\vdots \\
\vdots \\
\vdots \\
\vdots \\
\vdots\\
c_{N}
\end{array}
\right)
=
\left(
\begin{array}{c}
h \\
2h\\
\vdots\\
\vdots \\
\vdots \\
\vdots \\
\vdots \\
2h\\
h
\end{array}
\right)
\end{equation*}
$$
Modyfikacja URL (wierszy) (obl. we wsp. glob.)
- Warunek Dirichleta \( u(\xno{k})= U_k \) jest równoważny \( c_k=U_k \) (ponieważ \( c_k=u(\xno{k}) \))
- zastąpmy pierwszy wiersz równaniem \( c_0=0 \)
- zastąpmy ostatni wiersz równaniem \( c_N=D \)
$$
\begin{equation*}
\frac{1}{h}\left(
\begin{array}{ccccccccc}
h & 0 & 0
&\cdots &
\cdots & \cdots & \cdots &
\cdots & 0 \\
-1 & 2 & -1 & \ddots & & & & & \vdots \\
0 & -1 & 2 & -1 &
\ddots & & & & \vdots \\
\vdots & \ddots & & \ddots & \ddots & 0 & & & \vdots \\
\vdots & & \ddots & \ddots & \ddots & \ddots & \ddots & & \vdots \\
\vdots & & & 0 & -1 & 2 & -1 & \ddots & \vdots \\
\vdots & & & & \ddots & \ddots & \ddots &\ddots & 0 \\
\vdots & & & & &\ddots & \ddots &\ddots & -1 \\
0 &\cdots & \cdots &\cdots & \cdots & \cdots & 0 & 0 & h
\end{array}
\right)
\left(
\begin{array}{c}
c_0 \\
\vdots\\
\vdots\\
\vdots \\
\vdots \\
\vdots \\
\vdots \\
\vdots\\
c_{N}
\end{array}
\right)
=
\left(
\begin{array}{c}
0 \\
2h\\
\vdots\\
\vdots \\
\vdots \\
\vdots \\
\vdots \\
2h\\
D
\end{array}
\right)
\end{equation*}
$$
Modyfikacja URL; (obl. we wsp. lokalnych)
Na elemencie 0 znane jest \( u \) w węźle lokalnym o indeksie \( r=0 \)
->
Wymieńmy pierwsze równanie dla tego elementu na \( \tilde c_0 = 0 \):
$$
\begin{equation*}
\tilde A^{(0)} =
A = \frac{1}{h}\left(\begin{array}{rr}
h & 0\\
-1 & 1
\end{array}\right),\quad
\tilde b^{(0)} = \left(\begin{array}{c}
0\\
h
\end{array}\right)
\end{equation*}
$$
Na elemencie \( N_e \) znane jest \( u \) w węźle lokalnym o indeksie \( r=1 \)
->
Wymieńmy ostatnie równanie dla tego elementu na \( \tilde c_1 = D \):
$$
\begin{equation*}
\tilde A^{(N_e)} =
A = \frac{1}{h}\left(\begin{array}{rr}
1 & -1\\
0 & h
\end{array}\right),\quad
\tilde b^{(N_e)} = \left(\begin{array}{c}
h\\
D
\end{array}\right)
\end{equation*}
$$
Modyfikacja URL z zachowaniem symetrii układu; algorytm
- Przedstawiona modyfikacja niszczy symterię macierzy: np. \( A_{0,1}\neq A_{1,0} \)
- Symetria - pożądana własność URL (szczególnie dla zagadnień 2D i 3D) (szybsze obliczenia, mniejsze obciążenie pamięci)
- Można zmodyfikować URL tak, aby zachować symterię!
Algorytm:
- Odejmij od prawej strony kolumnę \( i \) pomnożoną przez \( U_i \)
- wyzeruj kolumnę \( i \) i wiersz \( i \)
- Przypisz wartość 1 do elementu \( A_{i,i} \)
- Przypisz \( b_i=U_i \)
Modyfikacja URL z zachowaniem symetrii układu; przykład
$$
\begin{equation*}
\frac{1}{h}\left(
\begin{array}{ccccccccc}
h & 0 & 0
&\cdots &
\cdots & \cdots & \cdots &
\cdots & 0 \\
0 & 2 & -1 & \ddots & & & & & \vdots \\
0 & -1 & 2 & -1 &
\ddots & & & & \vdots \\
\vdots & \ddots & & \ddots & \ddots & 0 & & & \vdots \\
\vdots & & \ddots & \ddots & \ddots & \ddots & \ddots & & \vdots \\
\vdots & & & 0 & -1 & 2 & -1 & \ddots & \vdots \\
\vdots & & & & \ddots & \ddots & \ddots &\ddots & 0 \\
\vdots & & & & &\ddots & \ddots &\ddots & 0 \\
0 &\cdots & \cdots &\cdots & \cdots & \cdots & 0 & 0 & h
\end{array}
\right)
\left(
\begin{array}{c}
c_0 \\
\vdots\\
\vdots\\
\vdots \\
\vdots \\
\vdots \\
\vdots \\
\vdots\\
c_{N}
\end{array}
\right)
=
\left(
\begin{array}{c}
0 \\
2h\\
\vdots\\
\vdots \\
\vdots \\
\vdots \\
\vdots \\
2h +\frac{D}{h}\\
D
\end{array}
\right)
\end{equation*}
$$
Modyfikacja URL z zachowaniem symetrii układu (wsp. lokalne)
Modyfikacja z zachowaniem symetrii zastosowana dla macierzy lokalnej \( \tilde A^{(N_e)} \):
$$
\begin{equation*}
\tilde A^{(N_e)} =
A = \frac{1}{h}\left(\begin{array}{rr}
1 & 0\\
0 & h
\end{array}\right),\quad
\tilde b^{(N_e)} = \left(\begin{array}{c}
h + D/h\\
D
\end{array}\right)
\end{equation*}
$$
Implementacja warunku Neumanna
Jak uwzględnić \( u'(0)=C \) w \( \FEM \)?
$$ -u''=f,\quad u'(0)=C,\ u(L)=D$$
- \( \baspsi_i(L)=0 \) ze względu na warunek Dirichleta \( u(L)=D \) (lub modyfikacja samego URL bez wymagań narzuconych na \( \baspsi \))
- Brak wymagań co do \( \baspsi_i(0) \)
- Warunek \( u'(0)=C \) można uwzględnić jak do tej pory, poprzez człon ''całkowo-brzegowy'' pochodzący z całkowania przez części
Sformułowanie wariacyjne
Metoda Galerkina:
$$
\begin{equation*}
\int_0^L(u''(x)+f(x))\baspsi_i(x) dx = 0,\quad i\in\If
\end{equation*}
$$
Całkowanie \( u''\baspsi_i \) przez części:
$$
\begin{equation*}
\int_0^Lu'(x)\baspsi_i'(x) \dx -(u'(L)\baspsi_i(L) - u'(0)\baspsi_i(0)) -
\int_0^L f(x)\baspsi_i(x) \dx =0
\end{equation*}
$$
- \( u'(L){\baspsi_i(L)}=0 \) ponieważ \( \baspsi_i(L)=0 \)
- \( u'(0)\baspsi_i(0) = C\baspsi_i(0) \) ponieważ \( u'(0)=C \)
Metoda 1: Zastosowanie funkcji brzegowej \( B(x) \) i usunięcie węzłów Dirichleta z URL
- \( \baspsi_i = \basphi_i \), \( i\in\If =\{0,\ldots,N=N_n-2\} \)
- \( B(x)=D\basphi_{N_n-1}(x) \), \( u= B + \sum_{j=0}^N c_j\basphi_j \)
$$
\begin{equation*}
\int_0^Lu'(x)\basphi_i'(x) dx =
\int_0^L f(x)\basphi_i(x) dx - C\basphi_i(0),\quad i\in\If
\end{equation*}
$$
$$
\begin{equation*}
\sum_{j=0}^{N}\left(
\int_0^L \basphi_i'\basphi_j' dx \right)c_j =
\int_0^L\left(f\basphi_i -D\basphi_N'\basphi_i\right) dx
- C\basphi_i(0)
\end{equation*}
$$
for \( i=0,\ldots,N=N_n-2 \).
Metoda 2: Wykorzystanie wszystkich \( \basphi_i \) i uwzględnienie warunku Dirichleta bezpośrednio w URL
- \( \baspsi_i=\basphi_i \), \( i=0,\ldots,N=N_n-1 \) (dla wszystkich węzłów)
- \( \basphi_N(L)\neq 0 \), więc \( u'(L)\basphi_N(L)\neq 0 \)
- Jednakże człon \( u'(L)\basphi_N(L) \) w \( b_N \) bedzie usunięty w momencie uwzględniania warunku Dirichleta \( b_N=D \)
Można zatem pominąć człon \( u'(L)\basphi_i(L) \)!
Składowe \( u'\basphi_i \) w węzłach \( \xno{i} \), w których wymuszamy warunek Dirichleta, mogą zostać pominięte.
\footnotesize \vspace{-0.3cm}
$$
\begin{equation*}
u(x) = \sum_{j=0}^{N=N_n-1} c_j\basphi_j(x)
\end{equation*}
$$
$$
\begin{equation*}
\sum_{j=0}^{N=N_n-1}\left(
\int_0^L \basphi_i'(x)\basphi_j'(x) dx \right)c_j =
\int_0^L f(x)\basphi_i(x) dx - C\basphi_i(0)
\end{equation*}
$$
\normalsize
Trzeba obliczyć wszystkie elementy dla \( i=0,\ldots,N=N_n-1 \), a następnie zmodyfikować ostatnie równanie do \( c_N=D \).
Wpływ warunku Neumanna na elementy macierzy A i wektora b
Dodatkowy człon \( C\basphi_0(0) \) ma wpływ jedynie na wektor prawej strony pierwszego elementu (\( \basphi_0=0 \) na wszystkich pozostałych elementach).
$$
\begin{equation*}
\tilde A^{(0)} =
A = \frac{1}{h}\left(\begin{array}{rr}
1 & 1\\
-1 & 1
\end{array}\right),\quad
\tilde b^{(0)} = \left(\begin{array}{c}
h - C\\
h
\end{array}\right)
\end{equation*}
$$
Algorytm metody elementów skończonych
Równanie różniczkowe definiuje całki sformułowania wariacyjnego.
Funkcje, które użytkownik musi podać na wejście programu:
integrand_lhs(phi, r, s, x)
boundary_lhs(phi, r, s, x)
integrand_rhs(phi, r, x)
boundary_rhs(phi, r, x)
(Ponadto potrzebna jest również informacja dotycząca siatki
zagadnienia, opisana przy pomocy struktur:
vertices, cells, oraz dof_map.
Pseudokod a'la Python; obliczenia dla elementu
<Declare global matrix, global rhs: A, b>
# Loop over all cells
for e in range(len(cells)):
# Compute element matrix and vector
n = len(dof_map[e]) # no of dofs in this element
h = vertices[cells[e][1]] - vertices[cells[e][0]]
<Declare element matrix, element vector: A_e, b_e>
# Integrate over the reference cell
points, weights = <numerical integration rule>
for X, w in zip(points, weights):
phi = <basis functions + derivatives at X>
detJ = h/2
x = <affine mapping from X>
for r in range(n):
for s in range(n):
A_e[r,s] += integrand_lhs(phi, r, s, x)*detJ*w
b_e[r] += integrand_rhs(phi, r, x)*detJ*w
# Add boundary terms
for r in range(n):
for s in range(n):
A_e[r,s] += boundary_lhs(phi, r, s, x)*detJ*w
b_e[r] += boundary_rhs(phi, r, x)*detJ*w
Pseudokod a'la Python; warunki brzegowe i assembling macierzy globalnych
for e in range(len(cells)):
...
# Incorporate essential boundary conditions
for r in range(n):
global_dof = dof_map[e][r]
if global_dof in essbc_dofs:
# dof r is subject to an essential condition
value = essbc_docs[global_dof]
# Symmetric modification
b_e -= value*A_e[:,r]
A_e[r,:] = 0
A_e[:,r] = 0
A_e[r,r] = 1
b_e[r] = value
# Assemble
for r in range(n):
for s in range(n):
A[dof_map[e][r], dof_map[e][r]] += A_e[r,s]
b[dof_map[e][r] += b_e[r]
<solve linear system>
Sformułowanie wariacyjne dla problemów 2D i 3D
- Całkowanie przez części - uogólnienie wzoru
- Inna geometria elementów (cell)
Całkowanie przez części
$$
\begin{equation*}
-\int_{\Omega} \nabla\cdot (\dfc(\x)\nabla u) v\dx =
\int_{\Omega} \dfc(\x)\nabla u\cdot\nabla v \dx -
\int_{\partial\Omega} a\frac{\partial u}{\partial n} v \ds
\end{equation*}
$$
- \( \int_\Omega ()\dx \): całka obszarowa (2D) lub objętościowa (3D)
- \( \int_{\partial\Omega} ()\ds \): całka krzywoliniowa (2D) lub obszarowa (3D)
- \( \partial\Omega_N \): warunki Neumanna \( -a\frac{\partial u}{\partial n} = g \)
- \( \partial\Omega_D \): warunki Dirichleta \( u = u_0 \)
- \( v\in V \) musi znikać na \( \partial\Omega_D \) (jeśli implementujemy metodę 1)
Całkowanie przez części; przykład
$$
\begin{align*}
\v\cdot\nabla u + \beta u &= \nabla\cdot\left( \dfc\nabla u\right) + f,
\quad & \x\in\Omega\\
u &= u_0,\quad &\x\in\partial\Omega_D\\
-\dfc\frac{\partial u}{\partial n} &= g,\quad &\x\in\partial\Omega_N
\end{align*}
$$
- Wiadome: \( \dfc \), \( \beta \), \( f \), \( u_0 \), oraz \( g \).
- Równanie różniczkowe drugiego rzędu: rozwiązywalne dla dokładnie jednego warunku brzegowego nakładanego w każdym węźle brzegowym.
Metoda 1 (funkcja brzegowa i \( \baspsi_i=0 \) na \( \partial\Omega_D \)) gwarantuje spełnienie warunku \( u=u_0 \):
$$ u(\x) = B(\x) + \sum_{j\in\If} c_j\baspsi_j(\x),\quad B(\x)=u_0(\x) $$
Całkowanie przez części w 1D/2D/3D
Metoda Galerkina: pomnóż przez \( v\in V \) i scałkuj nad \( \Omega \),
$$
\int_{\Omega} (\v\cdot\nabla u + \beta u)v\dx =
\int_{\Omega} \nabla\cdot\left( \dfc\nabla u\right)v\dx + \int_{\Omega}fv \dx
$$
Całkowanie przez części pierwszej całki po prawej stronie zgodnie ze wzorem:
$$
\int_{\Omega} \nabla\cdot\left( \dfc\nabla u\right) v \dx =
-\int_{\Omega} \dfc\nabla u\cdot\nabla v\dx
+ \int_{\partial\Omega} \dfc\frac{\partial u}{\partial n} v\ds,
$$
daje ostatecznie
$$
\int_{\Omega} (\v\cdot\nabla u + \beta u)v\dx =
-\int_{\Omega} \dfc\nabla u\cdot\nabla v\dx
+ \int_{\partial\Omega} \dfc\frac{\partial u}{\partial n} v\ds
+ \int_{\Omega} fv \dx
$$
Uwzględnianie warunku Neumanna w sformułowaniu wariacyjnym
Uwaga: \( v\neq 0 \) jedynie na \( \partial\Omega_N \) (ponieważ \( v=0 \) na \( \partial\Omega_D \)):
$$ \int_{\partial\Omega} \dfc\frac{\partial u}{\partial n} v\ds
= \int_{\partial\Omega_N} \underbrace{\dfc\frac{\partial u}{\partial n}}_{-g} v\ds
= -\int_{\partial\Omega_N} gv\ds
$$
Ostateczna postać sformułowania wariacyjnego:
$$
\int_{\Omega} (\v\cdot\nabla u + \beta u)v\dx =
-\int_{\Omega} \dfc\nabla u\cdot\nabla v \dx
- \int_{\partial\Omega_N} g v\ds
+ \int_{\Omega} fv \dx
$$
Równoważnie w notacji abstrakcyjnej:
$$
(\v\cdot\nabla u, v) + (\beta u,v) =
- (\dfc\nabla u,\nabla v) - (g,v)_{N} + (f,v)
$$
\( (g,v)_{N} \): całka krzywoliniowa (2D) lub powierzchniowa (3D) nad \( \partial\Omega_N \).
Etapy wyprowadzenia URL
- \( \forall v\in V \) jest zastępowana przez \( \baspsi_i \), \( i\in\If \)
- w sformułowaniu wariacyjnym uwzględnij \( u = B + \sum_{j\in\If} c_j\baspsi_j \), \( B = u_0 \),
- Określ odwzorowanie indeksów globalnych \( i,j \) oraz \( i \) (dla wektora prawej strony)
- Oblicz elementy URL \( \sum_{i\in\If}A_{i,j}c_j = b_i \), \( i\in\If \) wg wzorów
$$
A_{i,j} = (\v\cdot\nabla \baspsi_j, \baspsi_i) +
(\beta \baspsi_j ,\baspsi_i) + (\dfc\nabla \baspsi_j,\nabla \baspsi_i)
$$
$$
b_i = (g,\baspsi_i)_{N} + (f,\baspsi_i) -
(\v\cdot\nabla u_0, \baspsi_i) + (\beta u_0 ,\baspsi_i) +
(\dfc\nabla u_0,\nabla \baspsi_i)
$$
Tranformacja elementu unormowanego w 2D/3D (1)
Chcemy obliczyć całkę nad elementem całkując we współrzędnych unormowanych.
$$
\begin{equation*}
\int_{{\Omega}^{(e)}} \dfc(\x)\nabla\basphi_i\cdot\nabla\basphi_j\dx
\end{equation*}
$$
Odwzorowanie geometrii ze współrzędnych lokalnych (unormowanych) do współrzędnych globalnych:
$$ \x(\X) $$
gdzie Jakobian przekształcenia \( J \),
$$ J_{i,j}=\frac{\partial x_j}{\partial X_i} $$
Tranformacja elementu unormowanego w 2D/3D (2)
- pod całką zastępujemy \( \dx \rightarrow \det J\dX \).
- Trzeba wyrazić \( \nabla\basphi_i \) przy pomocy indeksacji lokalnej \( \refphi_r \), \( i=q(e,r) \): \( \nabla\refphi_r(\X) \)
- Potrzeba obliczyć \( \nabla_{\x}\refphi_r(\X) \) (pochodna względem \( \x \))
- Mamy tymczasem \( \nabla_{\X}\refphi_r(\X) \) (pochodną względem \( \X \))
- Potrzeba transformować \( \nabla_{\X}\refphi_r(\X) \) do \( \nabla_{\x}\refphi_r(\X) \)
Tranformacja elementu unormowanego w 2D/3D (3)
Znajdujemy:
$$
\begin{align*}
\nabla_{\X}\refphi_r &= J\cdot\nabla_{\x}\basphi_i\\
\nabla_{\x}\basphi_i &= \nabla_{\x}\refphi_r(\X)
= J^{-1}\cdot\nabla_{\X}\refphi_r(\X)
\end{align*}
$$
Transformacja całki ze współrzędnych globalnych do lokalnych:
$$
\begin{equation*}
\int_{\Omega^{(e)}} \dfc(\x)\nabla_{\x}\basphi_i\cdot\nabla_{\x}\basphi_j\dx =
\int_{\tilde\Omega^r} \dfc(\x(\X))(J^{-1}\cdot\nabla_{\X}\refphi_r)\cdot
(J^{-1}\cdot\nabla\refphi_s)\det J\dX
\end{equation*}
$$
Całkowanie numeryczne
Całkowanie numeryczne na unormowanym elemencie (trójkącie lub czworościanie)
$$ \int_{\tilde\Omega^r} g\dX = \sum_{j=0}^{n-1} w_j g(\bar\X_j)$$
Moduł numint.py zawiera różne kwadratury całkujące:
>>> import numint
>>> x, w = numint.quadrature_for_triangles(num_points=3)
>>> x
[(0.16666666666666666, 0.16666666666666666),
(0.66666666666666666, 0.16666666666666666),
(0.16666666666666666, 0.66666666666666666)]
>>> w
[0.16666666666666666, 0.16666666666666666, 0.16666666666666666]
- Element trójkątny: kwadratury dla \( n=1,3,4,7 \) pozwalają na całkowanie w sposób dokładny wielamianów stopnia odpowiednio \( 1,2,3,4 \).
- Element czworościenny: całkowanie wielomianów stopnia \( 1,2,3,4 \) w sposób ścisły jest możliwe gdy użyje się kwadratur stopnia \( n=1,4,5,11 \)