Metoda elementów skończonych - wstęp
Finite Element Method, FEM, MES
|
|
|
Finite Element Method, FEM, MES
|
|
|
|
|
|
Istnieje wiele wariantów i odmian \( \FEM \). Dzięki proponowanemu podejściu łatwiej się ''połapać''. Unikamy zamieszania wielością podejść do tematu, koncepcji i technicznych/implementacyjnych szczegółów.
Jak znaleźć wektor pewnej przestrzeni, który aproksymuje wektor przestrzeni o większym wymiarze?
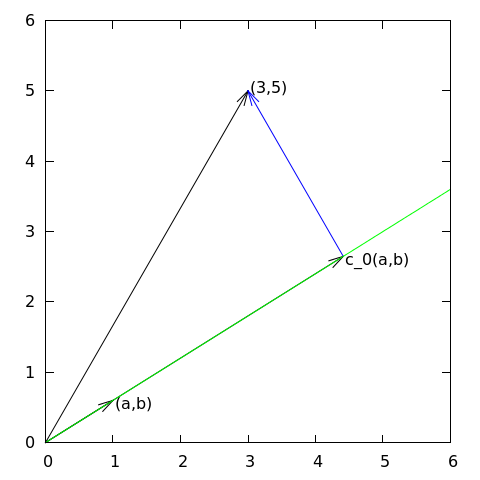
Ogólna idea poszukiwania elementu (wektora/funkcji) \( u(x) \) pewnej przestrzeni przybliżającego zadany element \( f(x) \):
$$
u(x) = \sum_{i=0}^N c_I \baspsi_i(x)
$$
gdzie
Sposób opisu i notacja zaproponowane w materiałach pozwalają na (nieco) łatwiejsze rozpoczęcie pracy i zrozumienie zasady działania wybrane w sposób ułatwiający zrozumienie open-source'owego pakietu FEniCS – biblioteki do obliczeń metodą elementów skończonych.
Zadanie:
Znajdź przybliżenie wektora \( \f = (3,5) \) wzdłuż zadanego kierunku.

analogie: element - punkt - wektor - funkcja
|
|
\( \quad \)
\( \quad \)
|
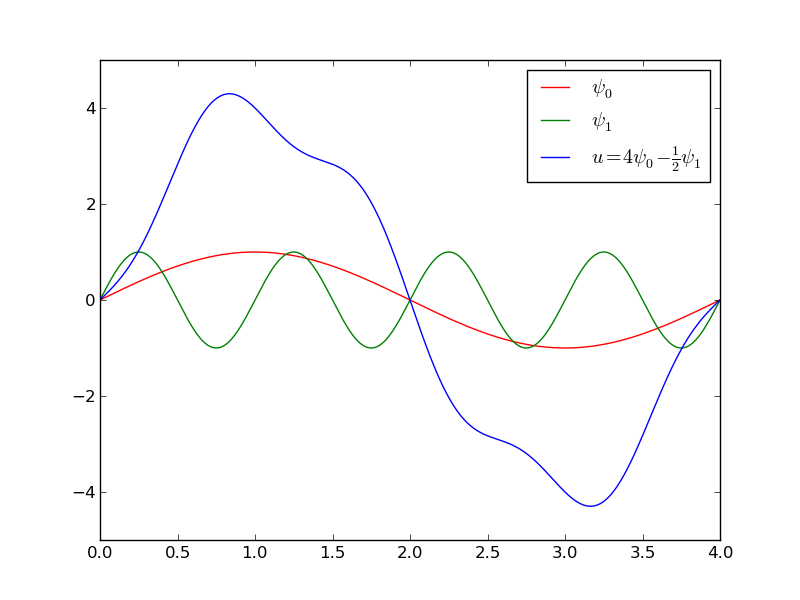
$$ V = \mbox{span}\,\{ \psib_0\} $$
Niech
\( (a,b) \) – punkt/wektor przestrzeni (dwuwymiarowej)
\( (\u,\v) \) – iloczyn skalarny dwóch wektorów przestrzeni (dowolnie-wymiarowej)
$$
\begin{equation*}
\frac{\partial E}{\partial c_0} = 0
\end{equation*}
$$
$$
\begin{align*}
E(c_0) &= (\e,\e) = (\f - \u, \f - \u) = (\f - c_0\psib_0, \f - c_0\psib_0)\\
&= (\f,\f) - 2c_0(\f,\psib_0) + c_0^2(\psib_0,\psib_0)
\end{align*}
$$
$$
\begin{equation}
\frac{\partial E}{\partial c_0} = -2(\f,\psib_0) + 2c_0 (\psib_0,\psib_0) = 0
\tag{1}
\end{equation}
$$
$$
c_0 = \frac{(\f,\psib_0)}{(\psib_0,\psib_0)} = \frac{3a + 5b}{a^2 + b^2}
$$
Spostrzeżenie (na później): warunek znikania pochodnej (1) można równoważnie zapisać jako:
$$ (\e, \psib_0) = 0 $$
$$
(\e, \psib_0) = (\f - \u, \psib_0) = (\f, \psib_0) - (\u, \psib_0) ....
\quad\quad (*-2 ...)
$$
$$
[\f-\u] \cdot
\left[
\begin{array}{c}
\\
\psib_0 \\
\\
\end{array}
\right]
=
[\quad\quad \f \quad\quad] \cdot
\left[
\begin{array}{c}
\\
\psib_0 \\
\\
\end{array}
\right]
-
[\quad\quad \u \quad\quad] \cdot
\left[
\begin{array}{c}
\\
\psib_0 \\
\\
\end{array}
\right]
$$
|
|
|
Dla danego wektora \( \f \), znajdź przybliżenie \( \u\in V \):
$$
\begin{equation*}
V = \hbox{span}\,\{\psib_0,\ldots,\psib_N\}
\end{equation*}
$$
(\( \hbox{span} \) czyt. przestrzeń rozpięta na wektorach...)
Mając dany zbiór wektorów niezależnych liniowo \( \psib_0,\ldots,\psib_N \), dowolny wektor \( \u\in V \) można zapisać jako:
$$ \u = \sum_{j=0}^Nc_j\psib_j$$
Wykazać, że przy pomocy kombinacji liniowej pewnych 3 wektorów przestrzeni 3D można skonstruować dowolny wektor tej przestrzeni.
Idea: znaleźć takie \( c_0,\ldots,c_N \), aby \( E= ||\e||^2 \) był minimalizowany, \( \e=\f-\u \).
$$
\begin{align*}
E(c_0,\ldots,c_N) &= (\e,\e) = (\f -\sum_jc_j\psib_j,\f -\sum_jc_j\psib_j)
\nonumber\\
&= (\f,\f) - 2\sum_{j=0}^Nc_j(\f,\psib_j) +
\sum_{p=0}^N\sum_{q=0}^N c_pc_q(\psib_p,\psib_q)
\end{align*}
$$
$$
\begin{equation*}
\frac{\partial E}{\partial c_i} = 0,\quad i=0,\ldots,N
\end{equation*}
$$
Po odrobinie obliczeń otrzymuje się układ równań liniowych:
$$
\begin{align}
\sum_{j=0}^N A_{i,j}c_j &= b_i,\quad i=0,\ldots,N
\tag{2}\\
A_{i,j} &= (\psib_i,\psib_j)
\tag{3}\\
b_i &= (\psib_i, \f)
\tag{4}
\end{align}
$$
Można pokazać, że poszukiwanie minimalnego \( ||\e|| \) jest równoważne poszukiwaniu \( \e \) ortogonalnego do wszystkich \( \v\in V \):
$$
(\e,\v)=0,\quad \forall\v\in V
$$
co jest równoważne temu aby \( \e \) był ortogonalny do każdego wektora bazowego:
$$ (\e,\psib_i)=0,\quad i=0,\ldots,N $$
Warunek ortogonalności – podstawa metody Galerkina. Generuje ten sam układ równań liniowych co \( \LSM \).
Niech \( V \) będzie przestrzenią funkcyjną rozpiętą na zbiorze funkcji bazowych \( \baspsi_0,\ldots,\baspsi_N \),
$$
\begin{equation*}
V = \hbox{span}\,\{\baspsi_0,\ldots,\baspsi_N\}
\end{equation*}
$$
Dowolną funkcję tej przestrzeni \( u\in V \) można przedstawić jako kombinację liniową funkcji bazowych:
$$ u = \sum_{j\in\If} c_j\baspsi_j,\quad\If = \{0,1,\ldots,N\} $$
Tak jak dla przestrzeni wektorowych, minimalizujemy normę błędu \( E \), ze względu na współczynniki \( c_j \), \( j\in\If \):
$$
E = (e,e) = (f-u,f-u) = \left(f(x)-\sum_{j\in\If} c_j\baspsi_j(x), f(x)-\sum_{j\in\If} c_j\baspsi_j(x)\right)
$$
$$ \frac{\partial E}{\partial c_i} = 0,\quad i=\in\If $$
Czym jest iloczyn skalarny jeśli \( \baspsi_i \) jest funkcją?
$$(f,g) = \int_\Omega f(x)g(x)\, dx$$
(iloczyn skalarny funkcji cg jako uogólnienie il. skalarnego funkcji dyskretnych \( (\u, \v) = \sum_j u_jv_j \))
$$
\begin{align*}
E(c_0,\ldots,c_N) &= (e,e) = (f-u,f-u) \\
&= (f,f) -2\sum_{j\in\If} c_j(f,\baspsi_i)
+ \sum_{p\in\If}\sum_{q\in\If} c_pc_q(\baspsi_p,\baspsi_q)
\end{align*}
$$
$$ \frac{\partial E}{\partial c_i} = 0,\quad i=\in\If $$
Obliczenia identyczne jak dla przypadku wektorowego -> w rezultacie otrzymujemy układ równań liniowych
$$
\sum_{j\in\If}^N A_{i,j}c_j = b_i,\ i\in\If,\quad
A_{i,j} = (\baspsi_i,\baspsi_j),\
b_i = (f,\baspsi_i)
$$
Jak poprzednio minimalizacja \( (e,e) \) jest równoważna
$$
(e,\baspsi_i)=0,\quad i\in\If
\tag{5}
$$
co z kolei jest równoważne
$$
(e,v)=0,\quad\forall v\in V
\tag{6}
$$
Równoważność wzorów jak dla przestrzeni wektorowych.
Równoważność wzorów jak dla wyprowadzenia przy pomocy \( \LSM \).
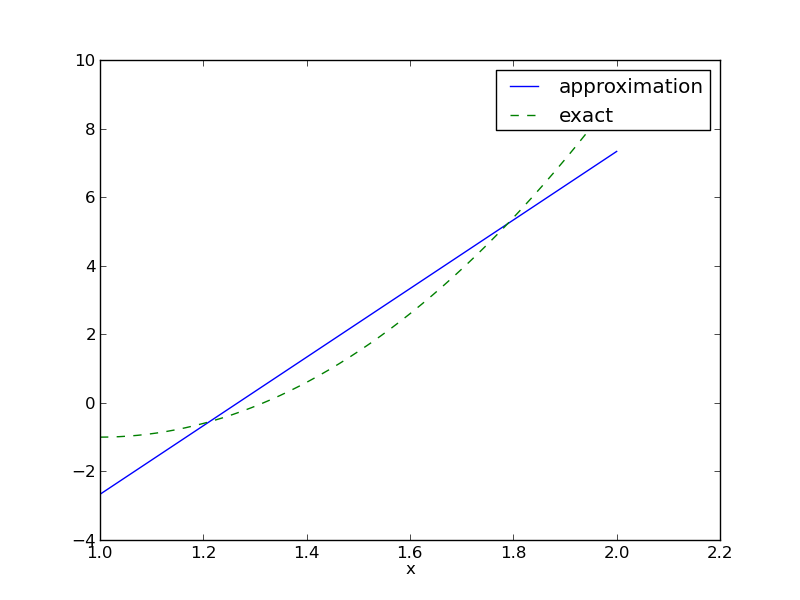
Dla zadanej funkcji \( f(x) = 10(x-1)^2 - 1 \) znaleźć jej przybliżenie funkcją liniową.
$$
\begin{equation*} V = \hbox{span}\,\{1, x\} \end{equation*}
$$
czyli \( \baspsi_0(x)=1 \), \( \baspsi_1(x)=x \) oraz \( N=1 \). Szukane
$$
\begin{equation*}
u=c_0\baspsi_0(x) + c_1\baspsi_1(x) = c_0 + c_1x
\end{equation*}
$$
$$
\begin{align*}
A_{0,0} &= (\baspsi_0,\baspsi_0) = \int_1^21\cdot 1\, dx = 1\\
A_{0,1} &= (\baspsi_0,\baspsi_1) = \int_1^2 1\cdot x\, dx = 3/2\\
A_{1,0} &= A_{0,1} = 3/2\\
A_{1,1} &= (\baspsi_1,\baspsi_1) = \int_1^2 x\cdot x\,dx = 7/3\\
b_1 &= (f,\baspsi_0) = \int_1^2 (10(x-1)^2 - 1)\cdot 1 \, dx = 7/3\\
b_2 &= (f,\baspsi_1) = \int_1^2 (10(x-1)^2 - 1)\cdot x\, dx = 13/3
\end{align*}
$$
Rozwiązanie układu równań 2x2:
$$ c_0 = -38/3,\quad c_1 = 10,\quad u(x) = 10x - \frac{38}{3} $$
$$
\begin{align*}
\left[
\begin{array}{cc}
1 & \frac{3}{2} \\
\frac{3}{2} & \frac{7}{3} \\
\end{array}
\right]
\left[
\begin{array}{c}
c_0 \\
c_1 \\
\end{array}
\right]
=
\left[
\begin{array}{c}
\frac{7}{3} \\
\frac{13}{3} \\
\end{array}
\right]
\quad
\rightarrow
\quad
\left[
\begin{array}{c}
c_0 \\
c_1 \\
\end{array}
\right]
=
\left[
\begin{array}{c}
-38/3 \\
10 \\
\end{array}
\right]
\end{align*}
$$
$$ u(x) = 10x - 12 \frac{2}{3} $$
Problem: napisać program/funkcję, który przeprowadzi obliczenia (obliczenie całek i rozwiązanie układu równań liniowych) i zwróci rozwiązanie postaci n \( u(x)=\sum_jc_j\baspsi_j(x) \).
Niech
sympy oznaczoną symbolem f (funkcję zmiennej (symbolu) x)psi będzie listą funkcji \( \sequencei{\baspsi} \),Omega będzie dwuelementową krotką/listą zawierającą początek i koniec przedziału \( \Omega \)import sympy as sym
def least_squares(f, psi, Omega):
N = len(psi) - 1
A = sym.zeros((N+1, N+1))
b = sym.zeros((N+1, 1))
x = sym.Symbol('x')
for i in range(N+1):
for j in range(i, N+1):
A[i,j] = sym.integrate(psi[i]*psi[j],
(x, Omega[0], Omega[1]))
A[j,i] = A[i,j]
b[i,0] = sym.integrate(psi[i]*f, (x, Omega[0], Omega[1]))
c = A.LUsolve(b)
u = 0
for i in range(len(psi)):
u += c[i,0]*psi[i]
return u, c
Spostrzeżenie: macierz układu jest symetryczna, dzięki czemu można zoptymalizować proces wyznaczania jej elementów
f) , sym.integrate zwróci wtedy obiekt typu sym.Integral. Ulepszenie kodu: sprawdzenie czy takie zdarzenie wystąpiło i ew. obliczenia numeryczne.def least_squares(f, psi, Omega, symbolic=True):
...
for i in range(N+1):
for j in range(i, N+1):
integrand = psi[i]*psi[j]
if symbolic:
I = sym.integrate(integrand, (x, Omega[0], Omega[1]))
if not symbolic or isinstance(I, sym.Integral):
# Could not integrate symbolically,
# fall back on numerical integration
integrand = sym.lambdify([x], integrand)
I = sym.mpmath.quad(integrand, [Omega[0], Omega[1]])
A[i,j] = A[j,i] = I
integrand = psi[i]*f
if symbolic:
I = sym.integrate(integrand, (x, Omega[0], Omega[1]))
if not symbolic or isinstance(I, sym.Integral):
integrand = sym.lambdify([x], integrand)
I = sym.mpmath.quad(integrand, [Omega[0], Omega[1]])
b[i,0] = I
...
Graficzne porównanie \( f \) i \( u \):
def comparison_plot(f, u, Omega, filename='tmp.pdf'):
x = sym.Symbol('x')
# Turn f and u to ordinary Python functions
f = sym.lambdify([x], f, modules="numpy")
u = sym.lambdify([x], u, modules="numpy")
resolution = 401 # no of points in plot
xcoor = linspace(Omega[0], Omega[1], resolution)
exact = f(xcoor)
approx = u(xcoor)
plot(xcoor, approx)
hold('on')
plot(xcoor, exact)
legend(['approximation', 'exact'])
savefig(filename)
>>> from approx1D import *
>>> x = sym.Symbol('x')
>>> f = 10*(x-1)**2-1
>>> u, c = least_squares(f=f, psi=[1, x], Omega=[1, 2])
>>> comparison_plot(f, u, Omega=[1, 2])

>>> from approx1D import *
>>> x = sym.Symbol('x')
>>> f = 10*(x-1)**2-1
>>> u, c = least_squares(f=f, psi=[1, x, x**2], Omega=[1, 2])
>>> print u
10*x**2 - 20*x + 9
>>> print sym.expand(f)
10*x**2 - 20*x + 9
Rozwiązanie przybliżone \( \equiv \) rozwiązanie dokładne, jeśli \( f \in V \)!
least_squares: dla \( i>2 \), \( c_i=0 \)
Jeśli \( f\in V \), \( \LSM \) oraz metoda Galerkina zwrócą \( u=f \).
Jeśli \( f\in V \), wtedy \( f=\sum_{j\in\If}d_j\baspsi_j \), dla pewnego \( \sequencei{d} \). Wtedy
$$
\begin{equation*}
b_i = (f,\baspsi_i) = \sum_{j\in\If}d_j(\baspsi_j, \baspsi_i)
= \sum_{j\in\If} d_jA_{i,j}
\end{equation*}
$$
a URL \( \sum_j A_{i,j}c_j = b_i \), \( i\in\If \), przedstawia sie:
$$
\begin{equation*}
\sum_{j\in\If}c_jA_{i,j} = \sum_{j\in\If}d_jA_{i,j},\quad i\in\If
\end{equation*}
$$
co oznacza, że \( c_i=d_i \) dla \( i\in\If \), czyli \( u \) jest tożsame z \( f \).
Poprzednie wnioski -> teoria i obliczenia symboliczne \ldots
Co w przypadku obliczeń numerycznych? -> (rozwiązanie URL macierzami liczb zmiennoprzecinkowych)
\( f \) to wciąż funkcja kwadratowa przybliżana przez
$$ u(x) = c_0 + c_1x + c_2x^2 + c_3x^3 +\cdots + c_Nx^N $$
Oczekiwane: \( c_2=c_3=\cdots=c_N=0 \), skoro \( f\in V \) oznacza \( u=f \).
A naprawdę?
| teoria | sympy | numpy32 | numpy64 |
|---|---|---|---|
| 9 | 9.62 | 5.57 | 8.98 |
| -20 | -23.39 | -7.65 | -19.93 |
| 10 | 17.74 | -4.50 | 9.96 |
| 0 | -9.19 | 4.13 | -0.26 |
| 0 | 5.25 | 2.99 | 0.72 |
| 0 | 0.18 | -1.21 | -0.93 |
| 0 | -2.48 | -0.41 | 0.73 |
| 0 | 1.81 | -0.013 | -0.36 |
| 0 | -0.66 | 0.08 | 0.11 |
| 0 | 0.12 | 0.04 | -0.02 |
| 0 | -0.001 | -0.02 | 0.002 |
matrix oraz lu_solve z biblioteki sympy.mpmath.fpnumpy 4B liczby zmiennoprzecinkowenumpy 8B liczby zmiennoprzecinkowe
Źródło kłopotów: funkcje \( x^i \) dla bardzo dużych \( i \) stają się praktycznie liniowo zależne
|
4 rozwiązania zadania przybliżenia paraboli
|
Wykresy funkcji \( x^i \) dla \( i=0 \ldots 14 \)
|
Aproksymacja funkcji \( f \) szeregiem Fouriera
$$ u(x) = \sum_i a_i\sin i\pi x = \sum_{j=0}^Nc_j\sin((j+1)\pi x) $$
to tylko ''zmiana bazy'':
$$
\begin{equation*}
V = \hbox{span}\,\{ \sin \pi x, \sin 2\pi x,\ldots,\sin (N+1)\pi x\}
\end{equation*}
$$
Obliczenia z wykorzystaniem funkcji least_squares:
N = 3
from sympy import sin, pi
psi = [sin(pi*(i+1)*x) for i in range(N+1)]
f = 10*(x-1)**2 - 1
Omega = [0, 1]
u, c = least_squares(f, psi, Omega)
comparison_plot(f, u, Omega)
L: \( N=3 \), P: \( N=11 \):
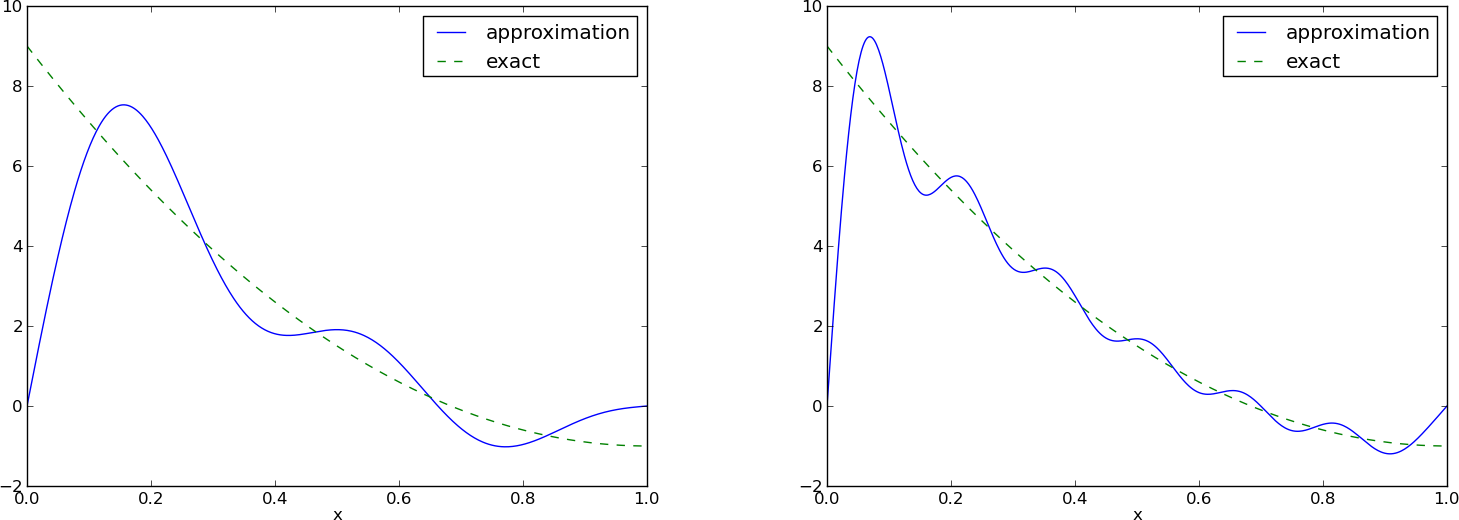
Dla każdej f.bazowej jest \( \baspsi_i(0)=0 \) przez co \( u(0)=0 \neq f(0)=9 \). Podobna sytuacja dla \( x=1 \). Wartości \( u \) na brzegach będą zawsze niepoprawne!
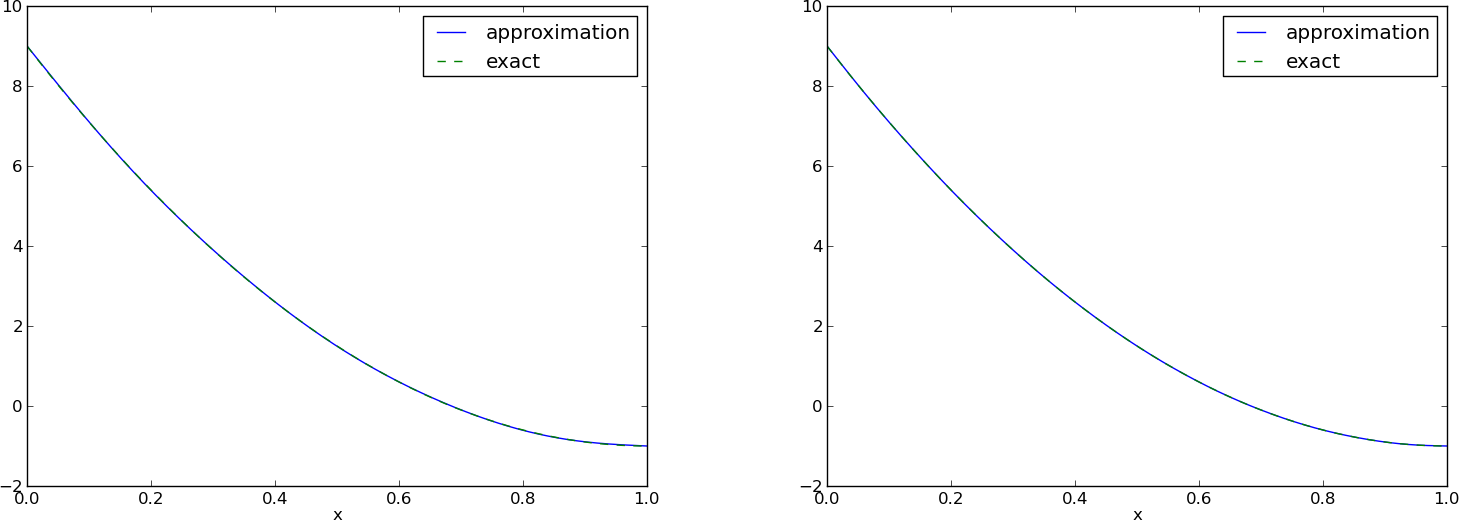
$$ u(x) = {\color{red}f(0)(1-x) + xf(1)} + \sum_{j\in\If} c_j\baspsi_j(x) $$
Dodatkowy wyraz nie tylko zapewnia \( u(0)=f(0) \) oraz \( u(1)=f(1) \), ale także zaskakująco dobrze poprawia jakość aproksymacji!
\( N=3 \) vs \( N=11 \):
Zalety wyboru funkcji sinus jako funkcji bazowych:
W ogólnym przypadku, dla baz ortogonalnych, \( A_{i,j} \) jest macierzą diagonalną, a nieznane współczynniki \( c_i \) można łatwo obliczyć:
$$
c_i = \frac{b_i}{A_{i,i}} = \frac{(f,\baspsi_i)}{(\baspsi_i,\baspsi_i)}
$$
def least_squares_orth(f, psi, Omega):
N = len(psi) - 1
A = [0]*(N+1)
b = [0]*(N+1)
x = sym.Symbol('x')
for i in range(N+1):
A[i] = sym.integrate(psi[i]**2, (x, Omega[0], Omega[1]))
b[i] = sym.integrate(psi[i]*f, (x, Omega[0], Omega[1]))
c = [b[i]/A[i] for i in range(len(b))]
u = 0
for i in range(len(psi)):
u += c[i]*psi[i]
return u, c
symbolic).sym.integrate zwraca sym.Integral), obliczenia wykonywane numerycznie (w przypadku funkcji sinus nie powinno być problemów z symbolicznym obliczeniem \( \int_\Omega\basphi_i^2dx \))
def least_squares_orth(f, psi, Omega, symbolic=True):
...
for i in range(N+1):
# Diagonal matrix term
A[i] = sym.integrate(psi[i]**2, (x, Omega[0], Omega[1]))
# Right-hand side term
integrand = psi[i]*f
if symbolic:
I = sym.integrate(integrand, (x, Omega[0], Omega[1]))
if not symbolic or isinstance(I, sym.Integral):
print 'numerical integration of', integrand
integrand = sym.lambdify([x], integrand)
I = sym.mpmath.quad(integrand, [Omega[0], Omega[1]])
b[i] = I
...
Inny sposób znalezienia przybliżenia \( f(x) \) przez \( u(x)=\sum_jc_j\baspsi_j \):
$$ u(\xno{i}) = \sum_{j\in\If} c_j \baspsi_j(\xno{i}) = f(\xno{i})
\quad i\in\If,N
$$
Współczynniki wygenerowanego układu równań to po prostu wartości funkcji, nie ma potrzeby całkowania!
$$
\begin{align}
\sum_{j\in\If} A_{i,j}c_j &= b_i,\quad i\in\If
\tag{7}\\
A_{i,j} &= \baspsi_j(\xno{i})
\tag{8}\\
b_i &= f(\xno{i})
\tag{9}
\end{align}
$$
W ogólnym przypadku macierz wynikowa niesymetryczna: \( \baspsi_j(\xno{i})\neq \baspsi_i(\xno{j}) \)
Zmienna points przechowuje punkty kolokacji
def interpolation(f, psi, points):
N = len(psi) - 1
A = sym.zeros((N+1, N+1))
b = sym.zeros((N+1, 1))
x = sym.Symbol('x')
# Turn psi and f into Python functions
psi = [sym.lambdify([x], psi[i]) for i in range(N+1)]
f = sym.lambdify([x], f)
for i in range(N+1):
for j in range(N+1):
A[i,j] = psi[j](points[i])
b[i,0] = f(points[i])
c = A.LUsolve(b)
u = 0
for i in range(len(psi)):
u += c[i,0]*psi[i](x)
return u
\( (4/3,5/3) \) vs \( (1,2) \):
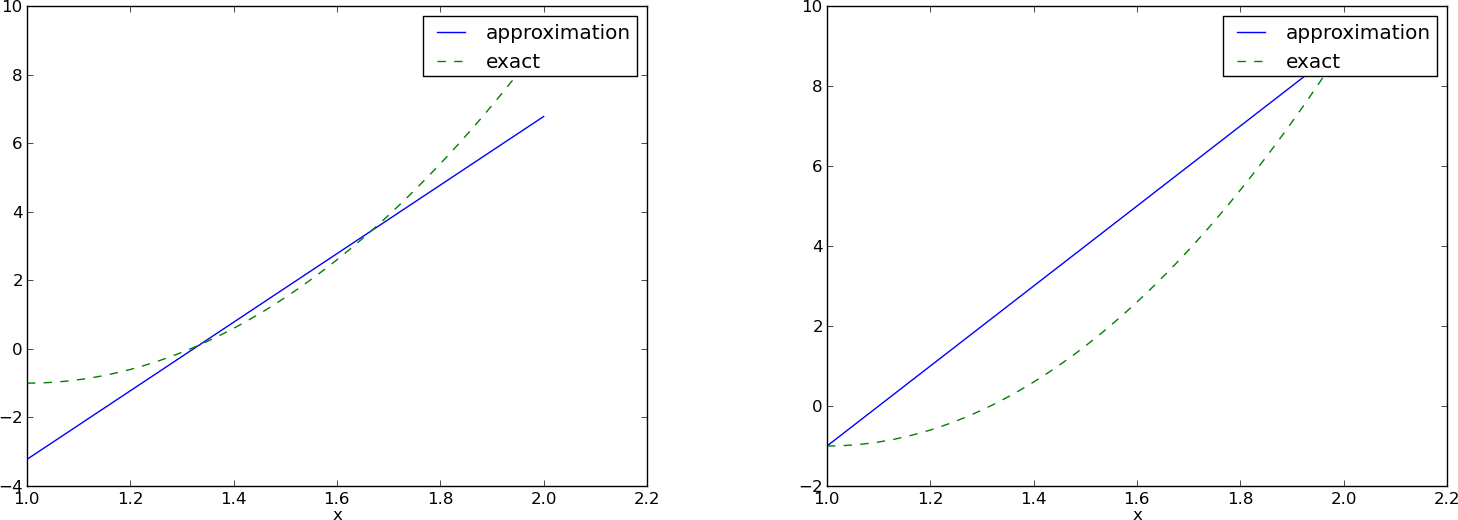

$$
u(\xno{i}) = \sum_{j\in\If} c_j \baspsi_j(\xno{i}) = f(\xno{i}),
\quad i=0,1,\ldots,m
$$
$$ \sum_{j\in\If} A_{i,j}c_j = b_i,\quad i=0,1,\ldots,m $$
$$ A_{i,j} = \baspsi_j(\xno{i}),\quad
b_i = f(\xno{i})$$
$$
\begin{align*}
B_{i,j} &= \sum_k A^T{i,k}A_{k,j} = \sum_k A{k,i}A_{k,j}
=\sum_{k=0}^m\baspsi_i(\xno{k}) \baspsi_j(\xno{k})
\\
d_i &=\sum_k A^T_{i,k}b_k = \sum_k A_{k,i}b_k =\sum_{k=0}^m
\baspsi_i(\xno{k})f(\xno{k})
\end{align*}
$$
def regression(f, psi, points):
N = len(psi) - 1
m = len(points)
# Use numpy arrays and numerical computing
B = np.zeros((N+1, N+1))
d = np.zeros(N+1)
# Wrap psi and f in Python functions rather than expressions
# so that we can evaluate psi at points[i]
x = sym.Symbol('x')
psi_sym = psi # save symbolic expression
psi = [sym.lambdify([x], psi[i]) for i in range(N+1)]
f = sym.lambdify([x], f)
for i in range(N+1):
for j in range(N+1):
B[i,j] = 0
for k in range(m+1):
B[i,j] += psi[i](points[k])*psi[j](points[k])
d[i] = 0
for k in range(m+1):
d[i] += psi[i](points[k])*f(points[k])
c = np.linalg.solve(B, d)
u = sum(c[i]*psi_sym[i] for i in range(N+1))
return u, c
import sympy as sym
x = sym.Symbol('x')
f = 10*(x-1)**2 - 1
psi = [1, x]
Omega = [1, 2]
m_values = [2-1, 8-1, 64-1]
# Create m+3 points and use the inner m+1 points
for m in m_values:
points = np.linspace(Omega[0], Omega[1], m+3)[1:-1]
u, c = regression(f, psi, points)
comparison_plot(f, u, Omega, points=points,
points_legend='%d interpolation points' % (m+1))
$$
\begin{align*}
u(x) &= 10x - 13.2,\quad 2\hbox{ punkty}\\
u(x) &= 10x - 12.7,\quad 8\hbox{ punktów}\\
u(x) &= 10x - 12.7,\quad 64\hbox{ punkty}
\end{align*}
$$

Motywacja::
Własność wielomianów Lagrange'a \( \baspsi_j \):
$$ \baspsi_i(\xno{j}) =\delta_{ij},\quad \delta_{ij} =
\left\lbrace\begin{array}{ll}
1, & i=j\\
0, & i\neq j
\end{array}\right.
$$
Zatem, \( c_i = f(x_i) \) and
$$
u(x) = \sum_{j\in\If} f(\xno{i})\baspsi_i(x)
$$
$$
\baspsi_i(x) =
\prod_{j=0,j\neq i}^N
\frac{x-\xno{j}}{\xno{i}-\xno{j}}
= \frac{x-x_0}{\xno{i}-x_0}\cdots\frac{x-\xno{i-1}}{\xno{i}-\xno{i-1}}\frac{x-\xno{i+1}}{\xno{i}-\xno{i+1}}
\cdots\frac{x-x_N}{\xno{i}-x_N}
$$
def Lagrange_polynomial(x, i, points):
p = 1
for k in range(len(points)):
if k != i:
p *= (x - points[k])/(points[i] - points[k])
return p
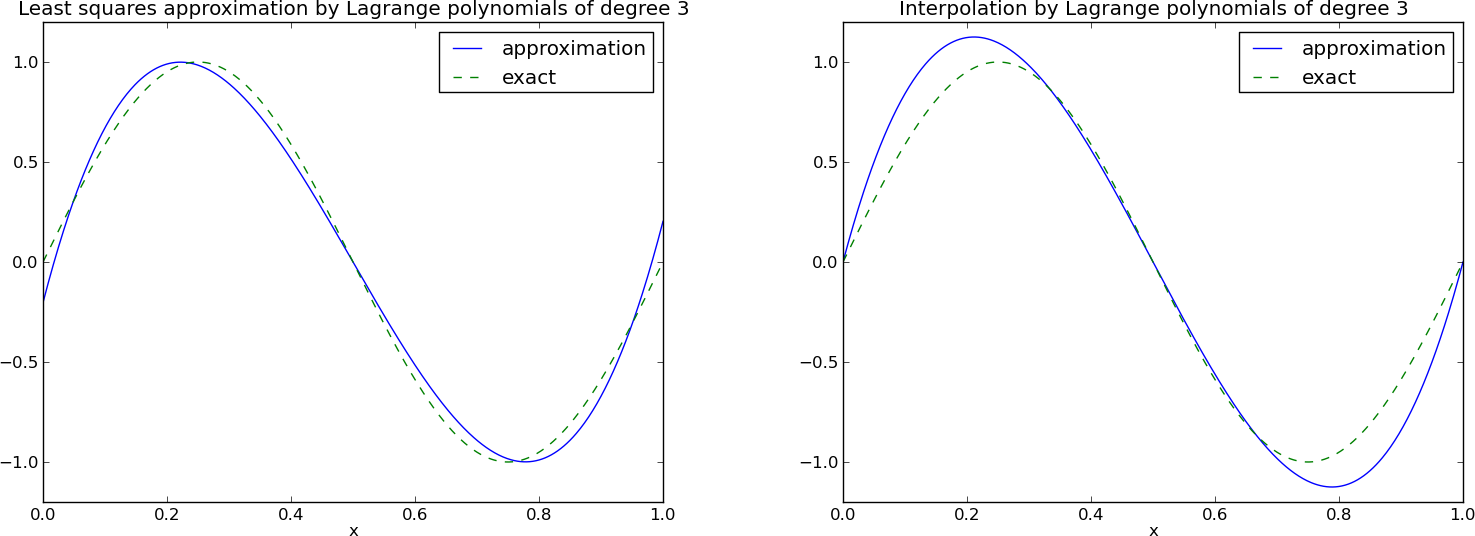
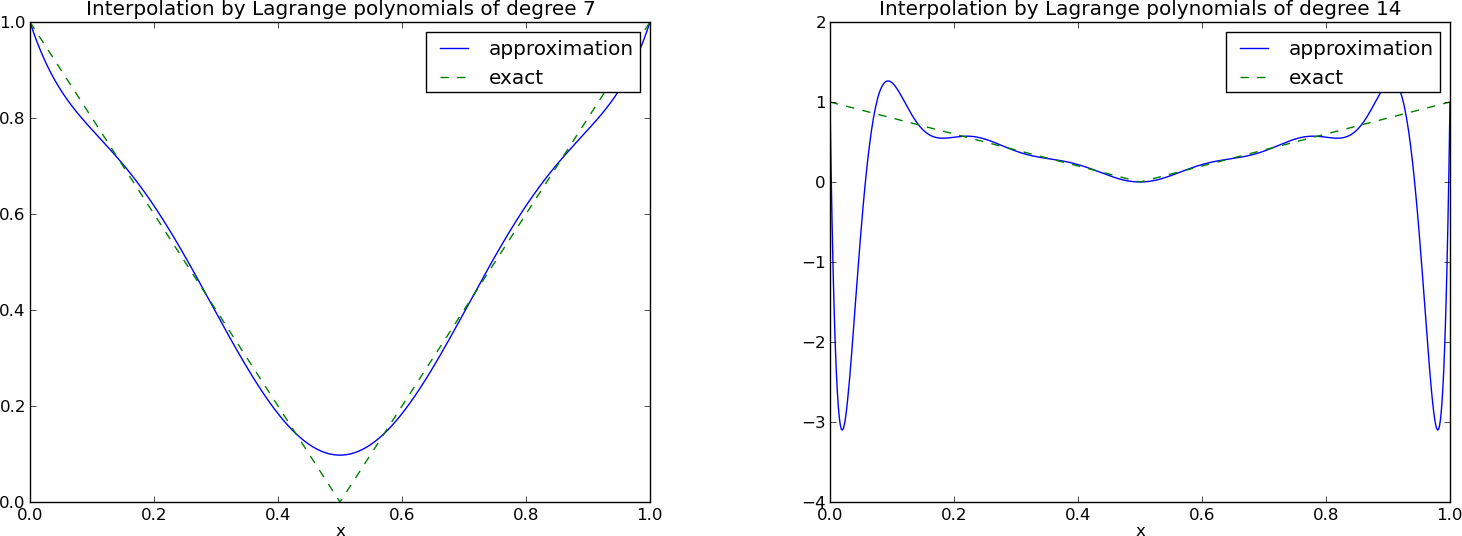
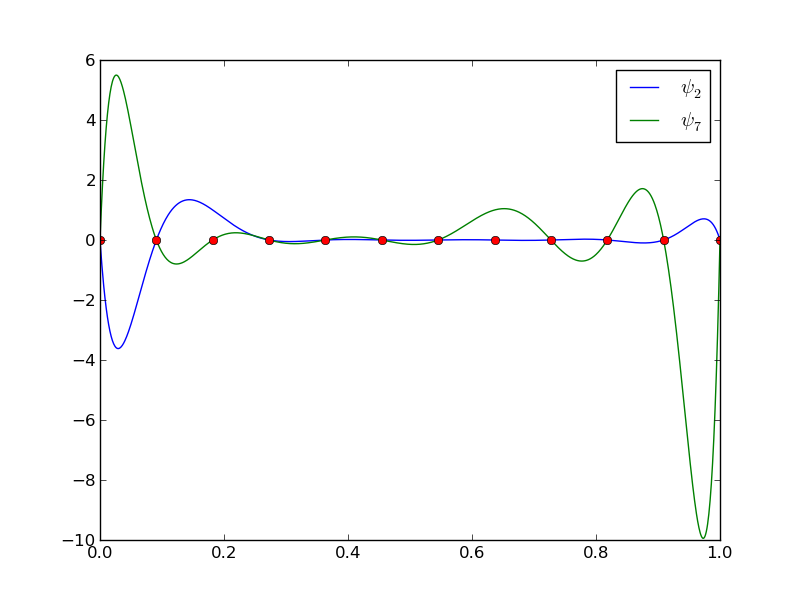
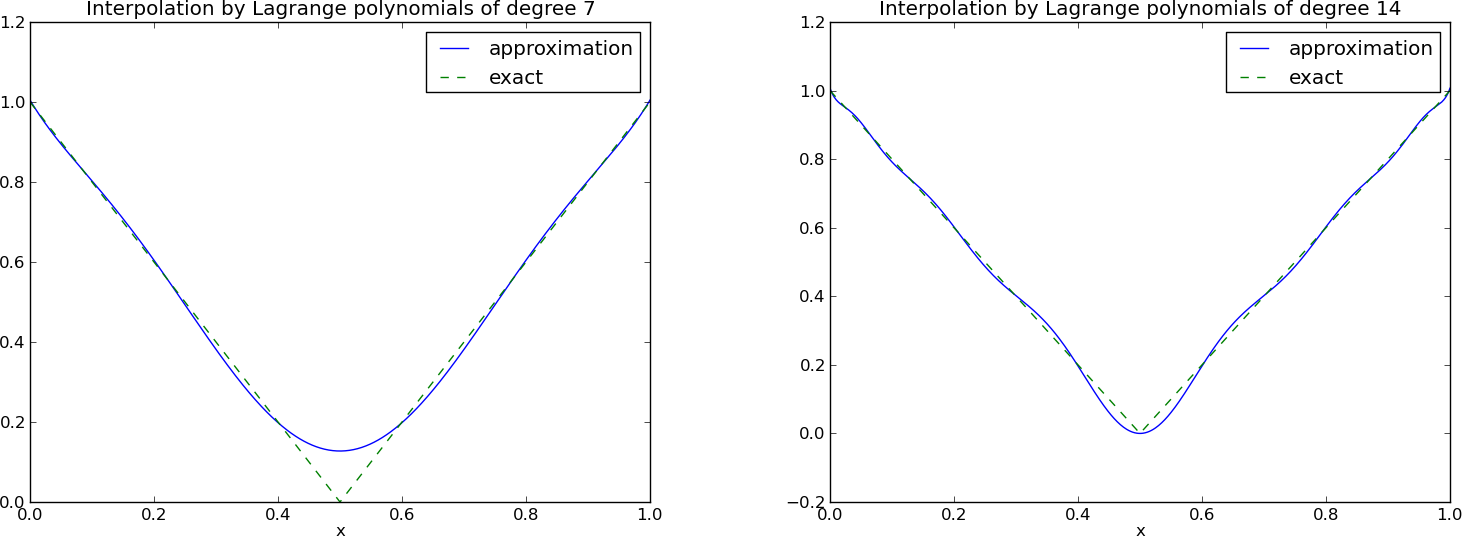
12 punktów, dwa wielomiany stopnia 11 (Uwaga!: \( \psi_2(x_2) \neq 0 \) i \( \psi_7(x_7) \neq 0 \)
Problem: oscylacje w okolicach krańców przedziałów dla większych \( N \).
Odpowiedni dobór węzłów interpolacji – węzły Czebyszewa:
$$
\xno{i} = \half (a+b) + \half(b-a)\cos\left( \frac{2i+1}{2(N+1)}\pi\right),\quad i=0\ldots,N
$$
na przedziale \( [a,b] \).
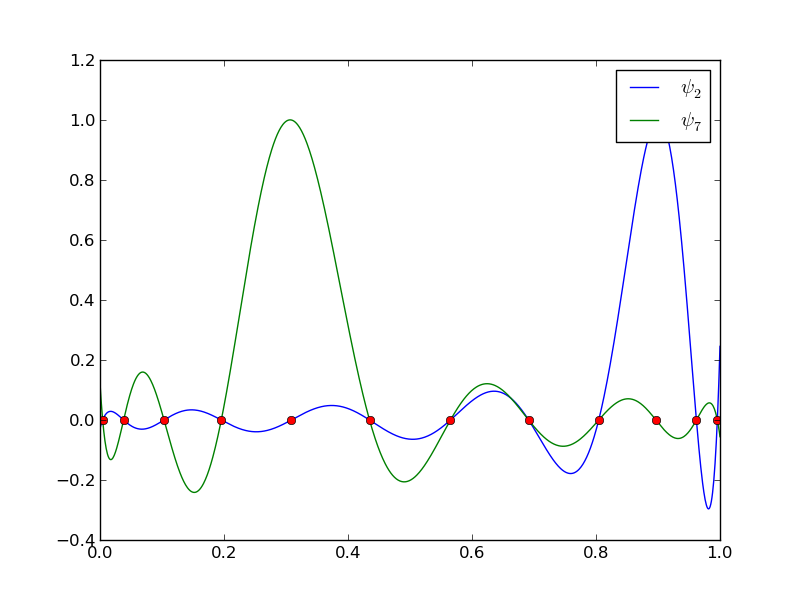
12 punktów, dwa wielomiany stopnia 11.
Uwaga!: Tym razem węzły są inaczej rozmieszczone!
Mniej oscylacyjny charakter wielomianów w porównaniu do węzłów równomiernie rozmieszczonych.
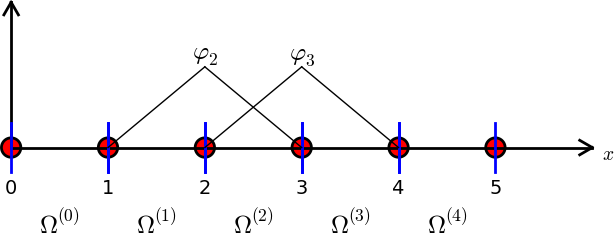
Nośnik funkcji: domknięcie zbioru argumentów funkcji, dla których ma ona wartość różną od zera (takie iksy dla których \( f(x) \neq 0 \))

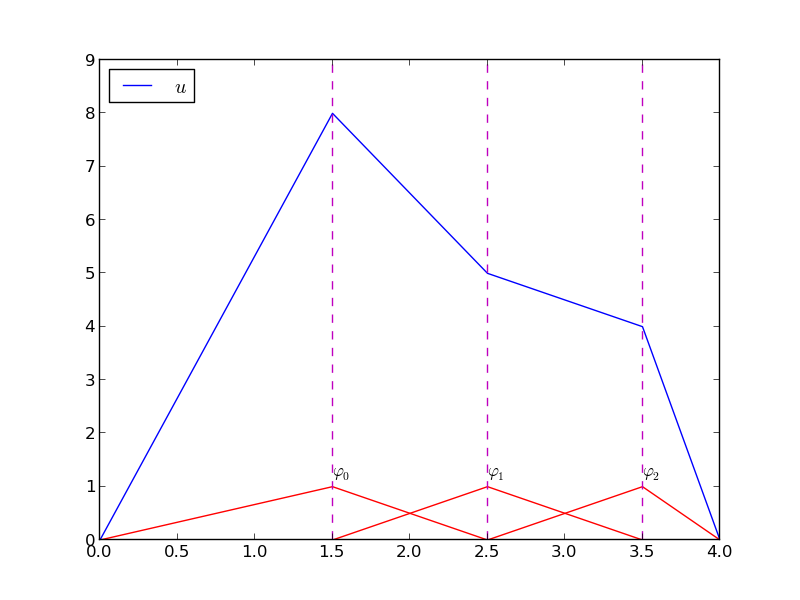
Podzielmy \( \Omega \) na \( N_e \) rozdzielnych podobszarów podobszarów – elementów:
$$
\Omega = \Omega^{(0)}\cup \cdots \cup \Omega^{(N_e)}
$$
Na każdym elemencie wprowadzamy \( N_n \) wezłów (punktów): \( \xno{0},\ldots,\xno{N_n-1} \)
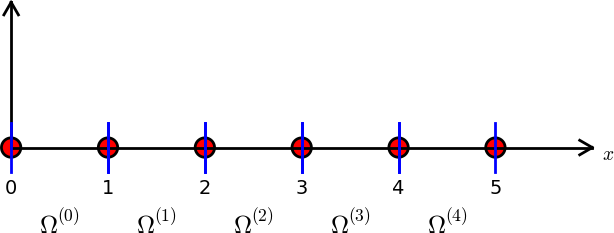
Struktura nodes – współrzędne węzłów.
Struktura elements – numery (globalne) węzłów tworzących
odpowiedni element.
nodes = [0, 1.2, 2.4, 3.6, 4.8, 5]
elements = [[0, 1], [1, 2], [2, 3], [3, 4], [4, 5]]

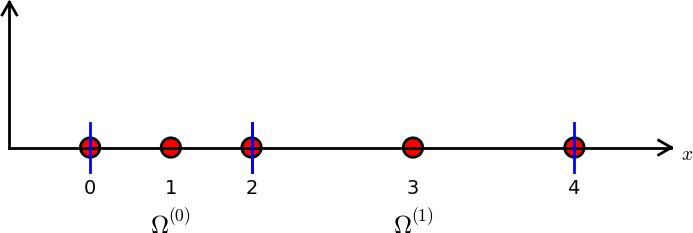
nodes = [0, 0.125, 0.25, 0.375, 0.5, 0.625, 0.75, 0.875, 1.0]
elements = [[0, 1, 2], [2, 3, 4], [4, 5, 6], [6, 7, 8]]
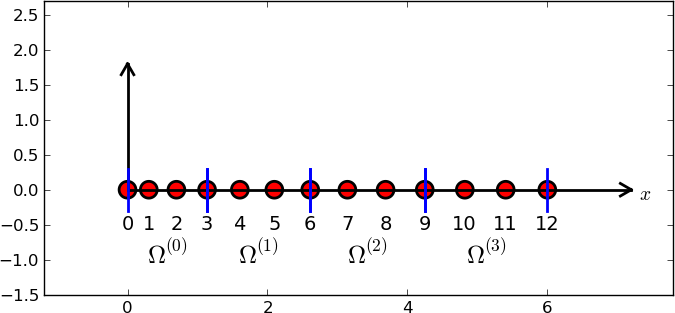
d = 3 # d+1 nodes per element
num_elements = 4
num_nodes = num_elements*d + 1
nodes = [i*0.5 for i in range(num_nodes)]
elements = [[i*d+j for j in range(d+1)] for i in range(num_elements)]
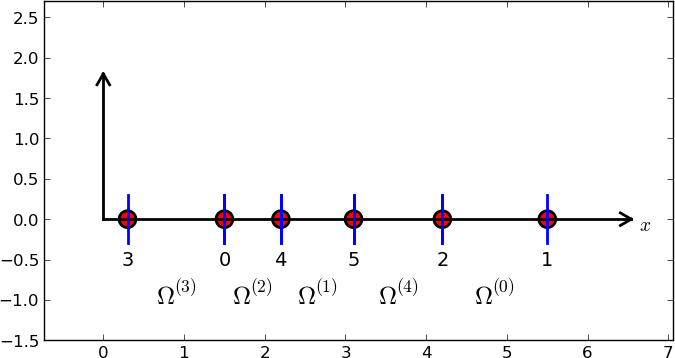
nodes = [1.5, 5.5, 4.2, 0.3, 2.2, 3.1]
elements = [[2, 1], [4, 5], [0, 4], [3, 0], [5, 2]]
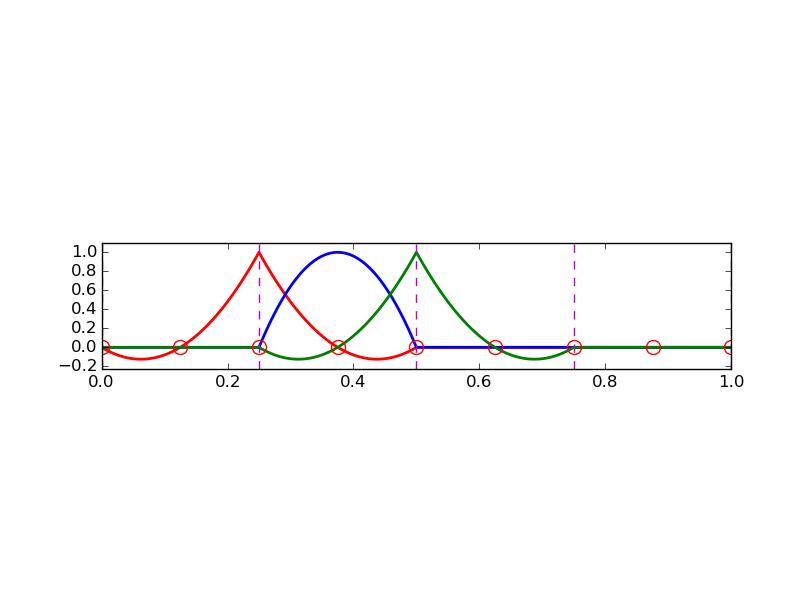
Ważna własność: \( c_i \) to wartość funkcji \( u \) w węźle \( i \), \( \xno{i} \):
$$
u(\xno{i}) = \sum_{j\in\If} c_j\basphi_j(\xno{i}) =
c_i\basphi_i(\xno{i}) = c_i
$$
Powód: \( \basphi_j(\xno{i}) =0 \) jeśli \( i\neq j \) i \( \basphi_i(\xno{i}) =1 \)
Ponieważ \( A_{i,j}=\int\basphi_i\basphi_j\dx \), większość współczynników macierzy będzie równa zero -> macierze rzadkie
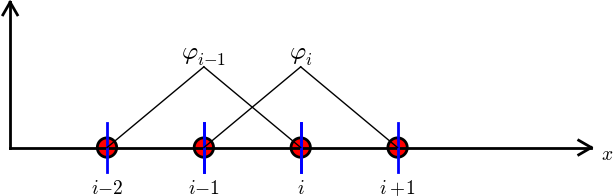

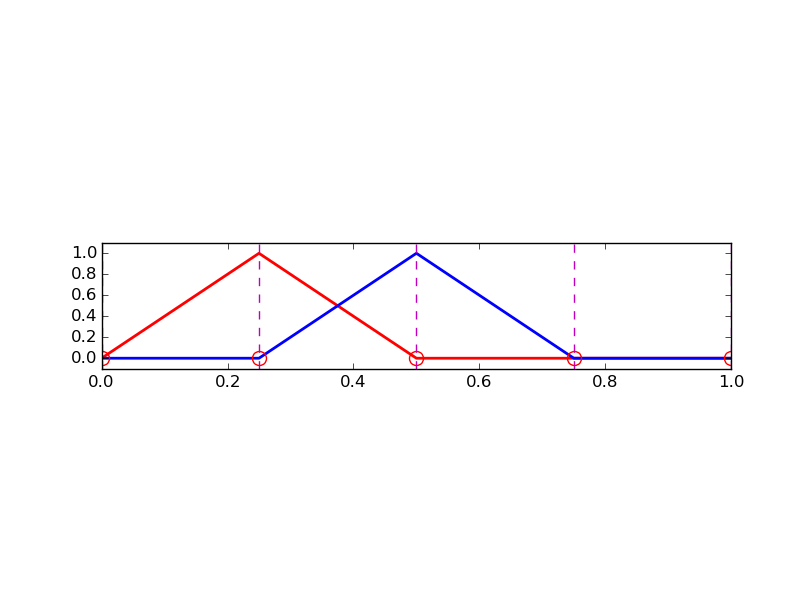
$$
\basphi_i(x) = \left\lbrace\begin{array}{ll}
0, & x < \xno{i-1}\\
(x - \xno{i-1})/h
& \xno{i-1} \leq x < \xno{i}\\
1 -
(x - x_{i})/h,
& \xno{i} \leq x < \xno{i+1}\\
0, & x\geq \xno{i+1}
\end{array}
\right.
$$



Uproszczenie: elementy jednakowej długości.
\( A_{2,3}=\int_\Omega\basphi_2\basphi_3 dx \): \( \basphi_2\basphi_3\neq 0 \) jedynie na elemencie 2. Dla tego elementu:
$$ \basphi_3(x) = (x-x_2)/h,\quad \basphi_2(x) = 1- (x-x_2)/h$$
$$
A_{2,3} = \int_\Omega \basphi_2\basphi_{3}\dx =
\int_{\xno{2}}^{\xno{3}}
\left(1 - \frac{x - \xno{2}}{h}\right) \frac{x - x_{2}}{h}
\dx = \frac{h}{6}
$$

$$ A_{2,2} =
\int_{\xno{1}}^{\xno{2}}
\left(\frac{x - \xno{1}}{h}\right)^2\dx +
\int_{\xno{2}}^{\xno{3}}
\left(1 - \frac{x - \xno{2}}{h}\right)^2\dx
= \frac{2h}{3}
$$

$$ A_{i,i-1} = \int_\Omega \basphi_i\basphi_{i-1}\dx = \hbox{?}$$
$$
\begin{align*}
A_{i,i-1} &= \int_\Omega \basphi_i\basphi_{i-1}\dx\\
&=
\underbrace{\int_{\xno{i-2}}^{\xno{i-1}} \basphi_i\basphi_{i-1}\dx}_{\basphi_i=0} +
\int_{\xno{i-1}}^{\xno{i}} \basphi_i\basphi_{i-1}\dx +
\underbrace{\int_{\xno{i}}^{\xno{i+1}} \basphi_i\basphi_{i-1}\dx}_{\basphi_{i-1}=0}\\
&= \int_{\xno{i-1}}^{\xno{i}}
\underbrace{\left(\frac{x - x_{i}}{h}\right)}_{\basphi_i(x)}
\underbrace{\left(1 - \frac{x - \xno{i-1}}{h}\right)}_{\basphi_{i-1}(x)} \dx =
\frac{h}{6}
\end{align*}
$$
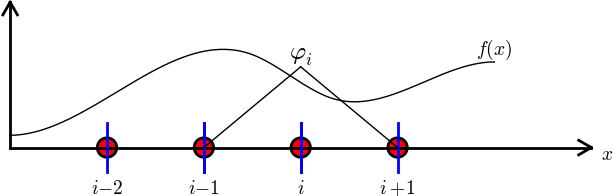
$$
b_i = \int_\Omega\basphi_i(x)f(x)\dx
= \int_{\xno{i-1}}^{\xno{i}} \frac{x - \xno{i-1}}{h} f(x)\dx
+ \int_{x_{i}}^{\xno{i+1}} \left(1 - \frac{x - x_{i}}{h}\right) f(x)
\dx
$$
Do dalszych obliczeń potrzebna konkretna postać \( f(x) \) ...
$$
\begin{equation*}
A = \frac{h}{6}\left(\begin{array}{ccc}
2 & 1 & 0\\
1 & 4 & 1\\
0 & 1 & 2
\end{array}\right),\quad
b = \frac{h^2}{12}\left(\begin{array}{c}
2 - 3h\\
12 - 14h\\
10 -17h
\end{array}\right)
\end{equation*}
$$
$$
\begin{equation*} c_0 = \frac{h^2}{6},\quad c_1 = h - \frac{5}{6}h^2,\quad
c_2 = 2h - \frac{23}{6}h^2
\end{equation*}
$$
$$
\begin{equation*} u(x)=c_0\basphi_0(x) + c_1\basphi_1(x) + c_2\basphi_2(x)\end{equation*}
$$

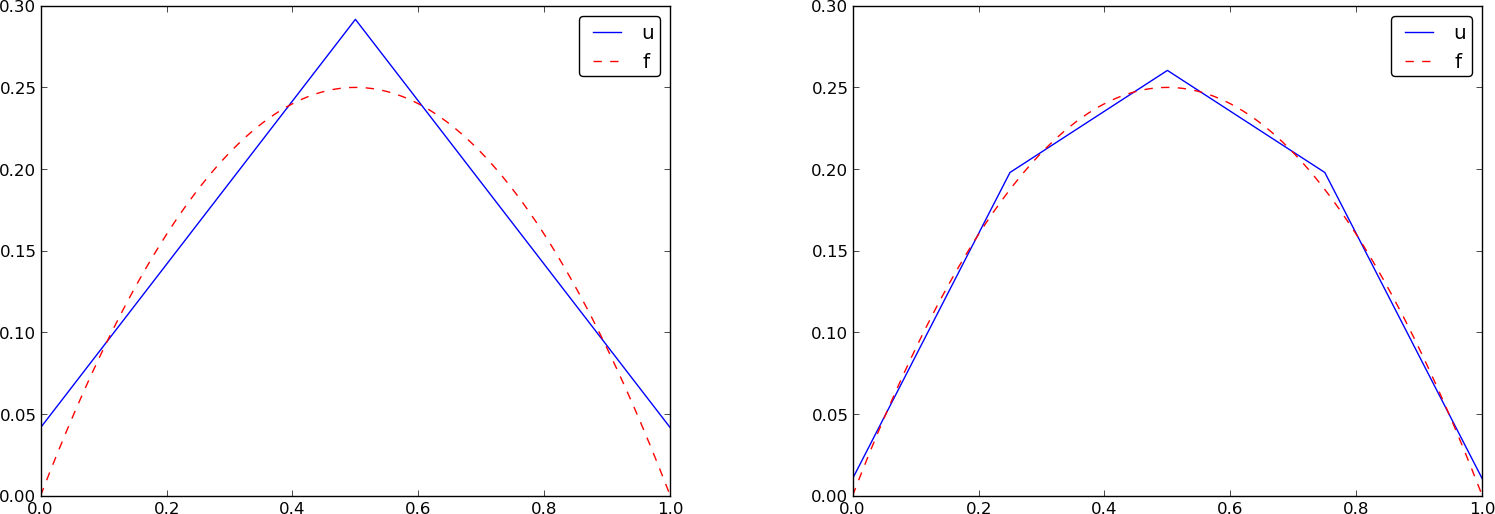
Przypomnienie: jeśli \( f\in V \), \( u \) odtworzy rozwiązanie bezbłędnie. Jeśli \( f \) to parabola, dowolna siatka elementów typu P2 (1 lub wiele elementów) sprawi wygeneruje \( u=f \). To samo dotyczyć będzie elementów typu P3, P4, itd., ponieważ one wszystkie potrafią odtworzyć wielomian 2. stopnia bezbłędnie.
(ang. assemble - gromadzić, składać, zbierać)
assembling, assemblacja?
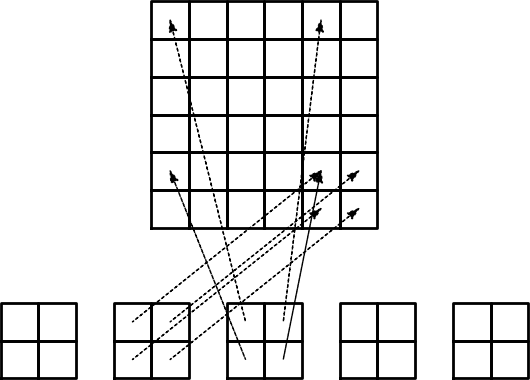
$$
A_{i,j} = \int_\Omega\basphi_i\basphi_jdx =
\sum_{e} \int_{\Omega^{(e)}} \basphi_i\basphi_jdx,\quad
A^{(e)}_{i,j}=\int_{\Omega^{(e)}} \basphi_i\basphi_jdx
$$
Ważne spostrzeżenia:

$$
\tilde A^{(e)} = \{ \tilde A^{(e)}_{r,s}\},\quad
\tilde A^{(e)}_{r,s} =
\int_{\Omega^{(e)}}\basphi_{q(e,r)}\basphi_{q(e,s)}dx,
\quad r,s\in\Ifd=\{0,\ldots,d\}
$$
|
|
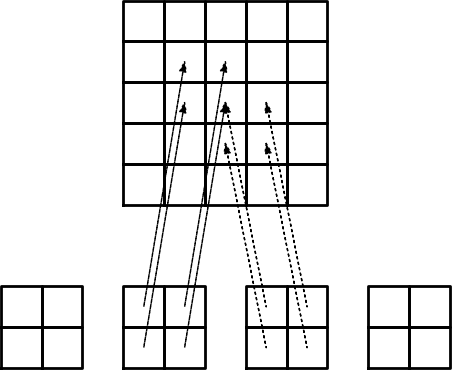
TODO
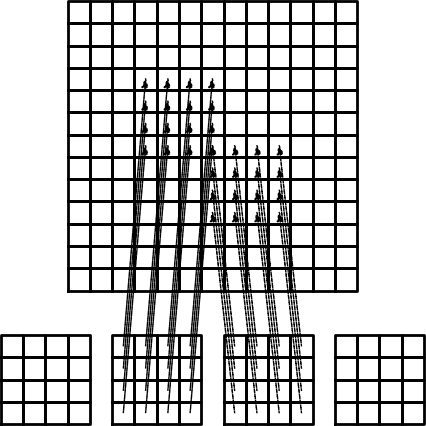
TODO

TODO
$$
b_i = \int_\Omega f(x)\basphi_i(x)dx =
\sum_{e} \int_{\Omega^{(e)}} f(x)\basphi_i(x)dx,\quad
b^{(e)}_{i}=\int_{\Omega^{(e)}} f(x)\basphi_i(x)dx
$$

Ważne spostrzeżenia:
Assembling:
$$
b_{q(e,r)} := b_{q(e,r)} + \tilde b^{(e)}_{r},\quad
r\in\Ifd
$$
Normalizacja współrzędnych położenia:
Zamiast całkować w granicach \( [x_L, x_R] \)
$$
\begin{equation*} \tilde A^{(e)}_{r,s} = \int_{\Omega^{(e)}}\basphi_{q(e,r)}(x)\basphi_{q(e,s)}(x)dx
= \int_{x_L}^{x_R}\basphi_{q(e,r)}(x)\basphi_{q(e,s)}(x)dx
\end{equation*}
$$
można transformować przedział \( [x_L, x_R] \) na przedział unormowany \( [-1,1] \) o współrzędnej lokalnej \( X \)
(Transformacja afiniczna)
$$
x = \half (x_L + x_R) + \half (x_R - x_L)X
$$
inaczej
$$
x = x_m + {\half}hX, \qquad x_m=(x_L+x_R)/2,\quad h=x_R-x_L
$$
Transformacja odwrotna:
$$
X = \frac{2 x + (x_L + x_R)}{(x_R - x_L)}
$$
Zmiana granic całkowania -> całkowanie na przedziale unormowanym: podstawienie \( x(X) \) w miejsce \( x \).
Lokalne funkcje bazowe we współrzędnych unormowanych:
$$
\refphi_r(X) = \basphi_{q(e,r)}(x(X))
$$
$$
\begin{array}{c}
x = \half (x_L + x_R) + \half (x_R - x_L)X \\
\downarrow \\
dx = \half (x_R - x_L) dX
\end{array}
$$
$$
\tilde A^{(e)}_{r,s}
=
\int_{\Omega^{(e)}}\basphi_{q(e,r)}(x)\basphi_{q(e,s)}(x)dx
=
\int\limits_{-1}^1 \refphi_r(X)\refphi_s(X)\underbrace{\frac{dx}{dX}}_{\det J= h/2}dX $$
$$
\tilde A^{(e)}_{r,s}
=
\int\limits_{-1}^1 \refphi_r(X)\refphi_s(X)\det J\,dX
$$
$$
\tilde b^{(e)}_{r} = \int_{\Omega^{(e)}}f(x)\basphi_{q(e,r)}(x)dx
= \int\limits_{-1}^1 f(x(X))\refphi_r(X)\det J\,dX
$$
$$
\begin{align}
\refphi_0(X) &= \half (1 - X)
\tag{10}\\
\refphi_1(X) &= \half (1 + X)
\tag{11}
\end{align}
$$
(proste funkcje wielomianowe zamiast definicji funkcji na podprzedziałach
$$
\begin{align}
\refphi_0(X) &= \half (X-1)X
\tag{12}\\
\refphi_1(X) &= 1 - X^2
\tag{13}\\
\refphi_2(X) &= \half (X+1)X
\tag{14}
\end{align}
$$
Łatwość wygenerowania elementów dowolnego rzędu... Jak?
Założenie: elementy typu P1, oraz funkcja \( f(x)=x(1-x) \).
$$
\begin{align}
\tilde A^{(e)}_{0,0}
&= \int_{-1}^1 \refphi_0(X)\refphi_0(X)\frac{h}{2} dX\nonumber\\
&=\int_{-1}^1 \half(1-X)\half(1-X) \frac{h}{2} dX =
\frac{h}{8}\int_{-1}^1 (1-X)^2 dX = \frac{h}{3}
\tag{15}\\
\tilde A^{(e)}_{1,0}
&= \int_{-1}^1 \refphi_1(X)\refphi_0(X)\frac{h}{2} dX\nonumber\\
&=\int_{-1}^1 \half(1+X)\half(1-X) \frac{h}{2} dX =
\frac{h}{8}\int_{-1}^1 (1-X^2) dX = \frac{h}{6}
\tag{16}\\
\tilde A^{(e)}_{0,1} &= \tilde A^{(e)}_{1,0}
\tag{17}\\
\tilde A^{(e)}_{1,1}
&= \int_{-1}^1 \refphi_1(X)\refphi_1(X)\frac{h}{2} dX\nonumber\\
&=\int_{-1}^1 \half(1+X)\half(1+X) \frac{h}{2} dX =
\frac{h}{8}\int_{-1}^1 (1+X)^2 dX = \frac{h}{3}
\tag{18}
\end{align}
$$
$$
\begin{align}
\tilde b^{(e)}_{0}
&= \int_{-1}^1 f(x(X))\refphi_0(X)\frac{h}{2} dX\nonumber\\
&= \int_{-1}^1 (x_m + \half hX)(1-(x_m + \half hX))
\half(1-X)\frac{h}{2} dX \nonumber\\
&= - \frac{1}{24} h^{3} + \frac{1}{6} h^{2} x_{m} - \frac{1}{12} h^{2} - \half h x_{m}^{2} + \half h x_{m}
\tag{19}\\
\tilde b^{(e)}_{1}
&= \int_{-1}^1 f(x(X))\refphi_1(X)\frac{h}{2} dX\nonumber\\
&= \int_{-1}^1 (x_m + \half hX)(1-(x_m + \half hX))
\half(1+X)\frac{h}{2} dX \nonumber\\
&= - \frac{1}{24} h^{3} - \frac{1}{6} h^{2} x_{m} + \frac{1}{12} h^{2} -
\half h x_{m}^{2} + \half h x_{m}
\tag{20}
\end{align}
$$
\( x_m \): środek elementu
>>> import sympy as sym
>>> x, x_m, h, X = sym.symbols('x x_m h X')
>>> sym.integrate(h/8*(1-X)**2, (X, -1, 1))
h/3
>>> sym.integrate(h/8*(1+X)*(1-X), (X, -1, 1))
h/6
>>> x = x_m + h/2*X
>>> b_0 = sym.integrate(h/4*x*(1-x)*(1-X), (X, -1, 1))
>>> print b_0
-h**3/24 + h**2*x_m/6 - h**2/12 - h*x_m**2/2 + h*x_m/2
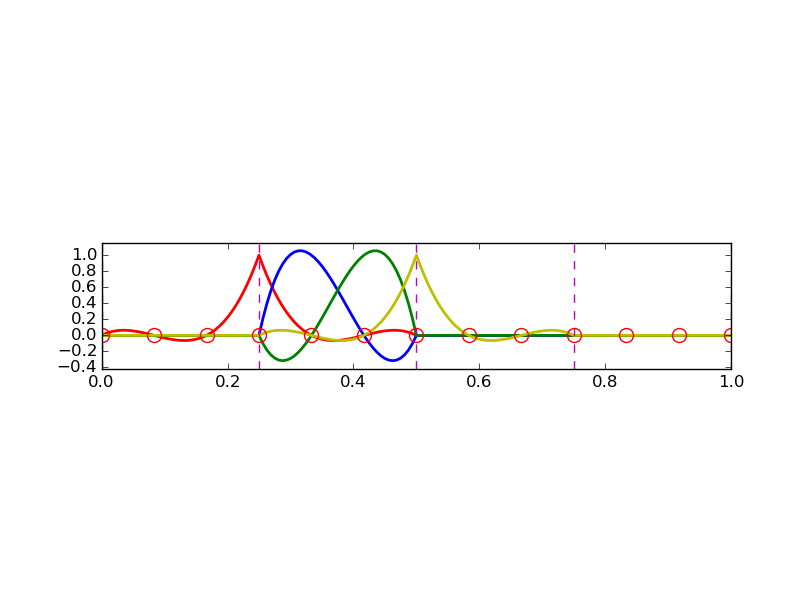
fe_approx1D.pyNiech \( \refphi_r(X) \) będzie wielomianem Lagrange'a stopnia d:
import sympy as sym
import numpy as np
def phi_r(r, X, d):
if isinstance(X, sym.Symbol):
h = sym.Rational(1, d) # node spacing
nodes = [2*i*h - 1 for i in range(d+1)]
else:
# assume X is numeric: use floats for nodes
nodes = np.linspace(-1, 1, d+1)
return Lagrange_polynomial(X, r, nodes)
def Lagrange_polynomial(x, i, points):
p = 1
for k in range(len(points)):
if k != i:
p *= (x - points[k])/(points[i] - points[k])
return p
def basis(d=1):
"""Return the complete basis."""
X = sym.Symbol('X')
phi = [phi_r(r, X, d) for r in range(d+1)]
return phi
def element_matrix(phi, Omega_e, symbolic=True):
n = len(phi)
A_e = sym.zeros((n, n))
X = sym.Symbol('X')
if symbolic:
h = sym.Symbol('h')
else:
h = Omega_e[1] - Omega_e[0]
detJ = h/2 # dx/dX
for r in range(n):
for s in range(r, n):
A_e[r,s] = sym.integrate(phi[r]*phi[s]*detJ, (X, -1, 1))
A_e[s,r] = A_e[r,s]
return A_e
>>> from fe_approx1D import *
>>> phi = basis(d=1)
>>> phi
[1/2 - X/2, 1/2 + X/2]
>>> element_matrix(phi, Omega_e=[0.1, 0.2], symbolic=True)
[h/3, h/6]
[h/6, h/3]
>>> element_matrix(phi, Omega_e=[0.1, 0.2], symbolic=False)
[0.0333333333333333, 0.0166666666666667]
[0.0166666666666667, 0.0333333333333333]
def element_vector(f, phi, Omega_e, symbolic=True):
n = len(phi)
b_e = sym.zeros((n, 1))
# Make f a function of X
X = sym.Symbol('X')
if symbolic:
h = sym.Symbol('h')
else:
h = Omega_e[1] - Omega_e[0]
x = (Omega_e[0] + Omega_e[1])/2 + h/2*X # mapping
f = f.subs('x', x) # substitute mapping formula for x
detJ = h/2 # dx/dX
for r in range(n):
b_e[r] = sym.integrate(f*phi[r]*detJ, (X, -1, 1))
return b_e
Zwróć uwagę na f.subs('x', x) -> podstawienie \( x(X) \) za x w formule na f
(od teraz f jest funkcją \( f(X) \))
sympy zawsze da radęsympy zwróci obiekt typu Integral zamiast liczby)
def element_vector(f, phi, Omega_e, symbolic=True):
...
I = sym.integrate(f*phi[r]*detJ, (X, -1, 1)) # try...
if isinstance(I, sym.Integral):
h = Omega_e[1] - Omega_e[0] # Ensure h is numerical
detJ = h/2
integrand = sym.lambdify([X], f*phi[r]*detJ)
I = sym.mpmath.quad(integrand, [-1, 1])
b_e[r] = I
...
def assemble(nodes, elements, phi, f, symbolic=True):
N_n, N_e = len(nodes), len(elements)
zeros = sym.zeros if symbolic else np.zeros
A = zeros((N_n, N_n))
b = zeros((N_n, 1))
for e in range(N_e):
Omega_e = [nodes[elements[e][0]], nodes[elements[e][-1]]]
A_e = element_matrix(phi, Omega_e, symbolic)
b_e = element_vector(f, phi, Omega_e, symbolic)
for r in range(len(elements[e])):
for s in range(len(elements[e])):
A[elements[e][r],elements[e][s]] += A_e[r,s]
b[elements[e][r]] += b_e[r]
return A, b
if symbolic:
c = A.LUsolve(b) # sympy arrays, symbolic Gaussian elim.
else:
c = np.linalg.solve(A, b) # numpy arrays, numerical solve
Uwaga: obliczanie współczynników macierzy A, b oraz rozwiązanie URL
A.LUsolve(b) może być baaardzo czasochłonne$\ldots$
>>> h, x = sym.symbols('h x')
>>> nodes = [0, h, 2*h]
>>> elements = [[0, 1], [1, 2]]
>>> phi = basis(d=1)
>>> f = x*(1-x)
>>> A, b = assemble(nodes, elements, phi, f, symbolic=True)
>>> A
[h/3, h/6, 0]
[h/6, 2*h/3, h/6]
[ 0, h/6, h/3]
>>> b
[ h**2/6 - h**3/12]
[ h**2 - 7*h**3/6]
[5*h**2/6 - 17*h**3/12]
>>> c = A.LUsolve(b)
>>> c
[ h**2/6]
[12*(7*h**2/12 - 35*h**3/72)/(7*h)]
[ 7*(4*h**2/7 - 23*h**3/21)/(2*h)]
>>> nodes = [0, 0.5, 1]
>>> elements = [[0, 1], [1, 2]]
>>> phi = basis(d=1)
>>> x = sym.Symbol('x')
>>> f = x*(1-x)
>>> A, b = assemble(nodes, elements, phi, f, symbolic=False)
>>> A
[ 0.166666666666667, 0.0833333333333333, 0]
[0.0833333333333333, 0.333333333333333, 0.0833333333333333]
[ 0, 0.0833333333333333, 0.166666666666667]
>>> b
[ 0.03125]
[0.104166666666667]
[ 0.03125]
>>> c = A.LUsolve(b)
>>> c
[0.0416666666666666]
[ 0.291666666666667]
[0.0416666666666666]
>>> d=1; N_e=8; Omega=[0,1] # 8 linear elements on [0,1]
>>> phi = basis(d)
>>> f = x*(1-x)
>>> nodes, elements = mesh_symbolic(N_e, d, Omega)
>>> A, b = assemble(nodes, elements, phi, f, symbolic=True)
>>> A
[h/3, h/6, 0, 0, 0, 0, 0, 0, 0]
[h/6, 2*h/3, h/6, 0, 0, 0, 0, 0, 0]
[ 0, h/6, 2*h/3, h/6, 0, 0, 0, 0, 0]
[ 0, 0, h/6, 2*h/3, h/6, 0, 0, 0, 0]
[ 0, 0, 0, h/6, 2*h/3, h/6, 0, 0, 0]
[ 0, 0, 0, 0, h/6, 2*h/3, h/6, 0, 0]
[ 0, 0, 0, 0, 0, h/6, 2*h/3, h/6, 0]
[ 0, 0, 0, 0, 0, 0, h/6, 2*h/3, h/6]
[ 0, 0, 0, 0, 0, 0, 0, h/6, h/3]
Uwaga (zadanie domowe): Wykonaj obliczenia na kartce papieru w celu potwierdzenia wartości poszczególnych elementów powyższej macierzy (pomocne w zrozumieniu materiału).
$$
A = \frac{h}{6}
\left(
\begin{array}{cccccccccc}
2 & 1 & 0
&\cdots & \cdots & \cdots & \cdots & \cdots & 0 \\
1 & 4 & 1 & \ddots & & & & & \vdots \\
0 & 1 & 4 & 1 &
\ddots & & & & \vdots \\
\vdots & \ddots & & \ddots & \ddots & 0 & & & \vdots \\
\vdots & & \ddots & \ddots & \ddots & \ddots & \ddots & & \vdots \\
\vdots & & & 0 & 1 & 4 & 1 & \ddots & \vdots \\
\vdots & & & & \ddots & \ddots & \ddots &\ddots & 0 \\
\vdots & & & & &\ddots & 1 & 4 & 1 \\
0 &\cdots & \cdots &\cdots & \cdots & \cdots & 0 & 1 & 2
\end{array}
\right)
$$
$$
A = \frac{h}{30}
\left(
\begin{array}{ccccccccc}
4 & 2 & - 1 & 0
& 0 & 0 & 0 & 0 & 0\\
2 & 16 & 2
& 0 & 0 & 0 & 0 & 0 & 0\\- 1 & 2 &
8 & 2 & - 1 & 0 & 0 & 0 & 0\\
0 & 0 & 2 & 16 & 2 & 0 & 0 & 0 & 0\\
0 & 0 & - 1 & 2 & 8 & 2 & - 1 & 0 & 0\\
0 & 0 & 0 & 0 & 2 & 16 & 2 & 0 & 0\\
0 & 0 & 0 & 0 & - 1 & 2 & 8 & 2 & - 1
\\0 & 0 & 0 & 0 & 0 & 0 &
2 & 16 & 2\\0 & 0 & 0 & 0 & 0
& 0 & - 1 & 2 & 4
\end{array}
\right)
$$
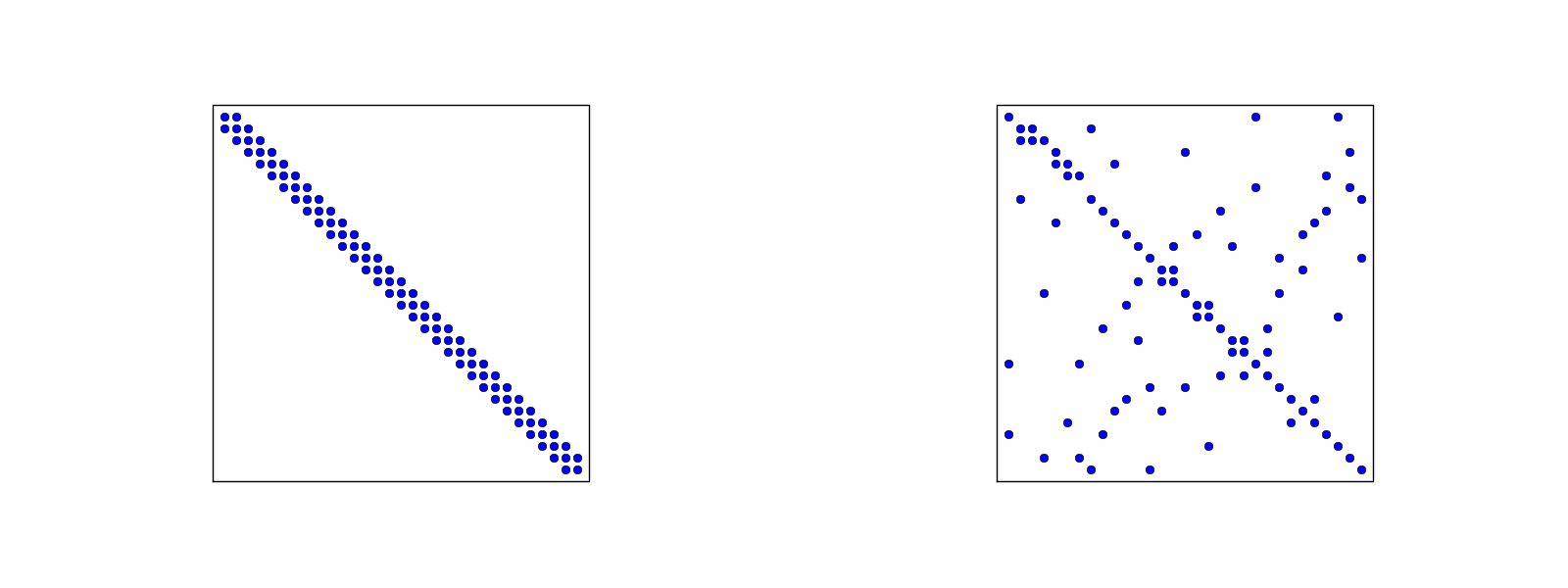
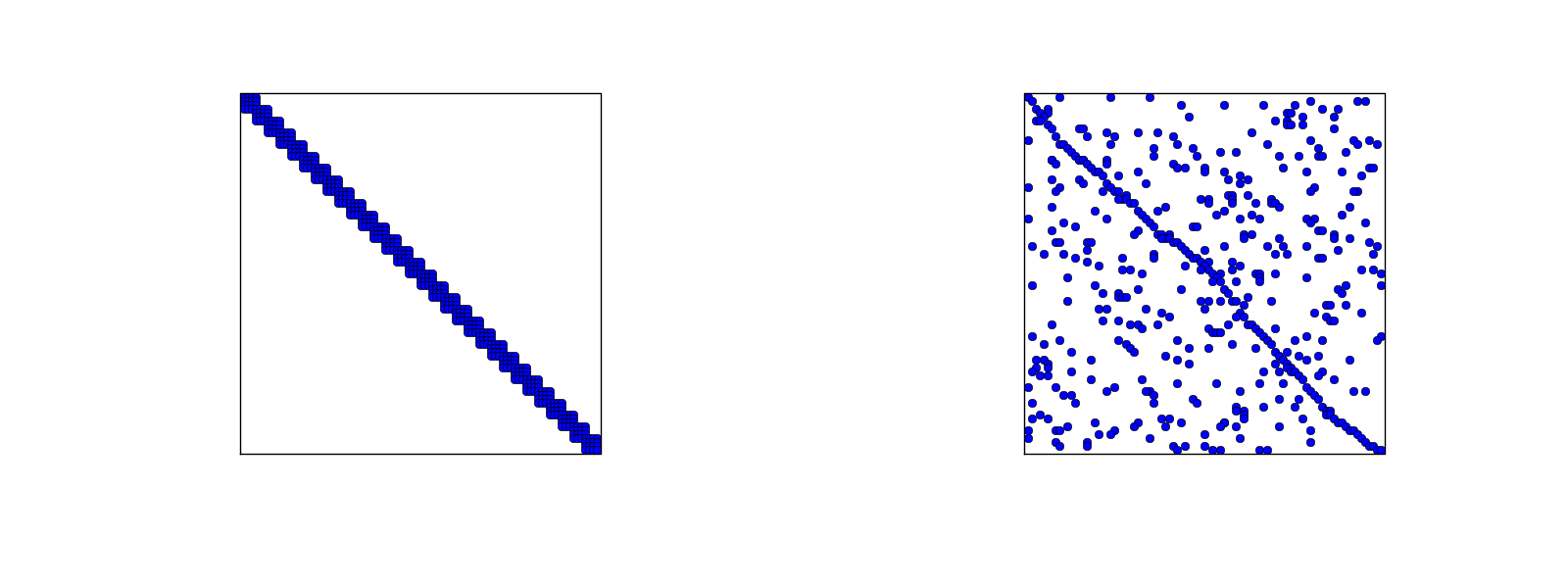
Postać specyficznych macierzy \( A_{i,j} \):
Wskazówki:
scipy.sparseZadanie: Porównać rozwiązanie zadania przybliżenia funkcji \( f(x) \) przy pomocy siatki \( N_e \) elementów skończonych o funkcjach bazowych rzędu \( d \).
import sympy as sym
from fe_approx1D import approximate
x = sym.Symbol('x')
approximate(f=x*(1-x)**8, symbolic=False, d=1, N_e=4)
approximate(f=x*(1-x)**8, symbolic=False, d=2, N_e=2)
approximate(f=x*(1-x)**8, symbolic=False, d=1, N_e=8)
approximate(f=x*(1-x)**8, symbolic=False, d=2, N_e=4)
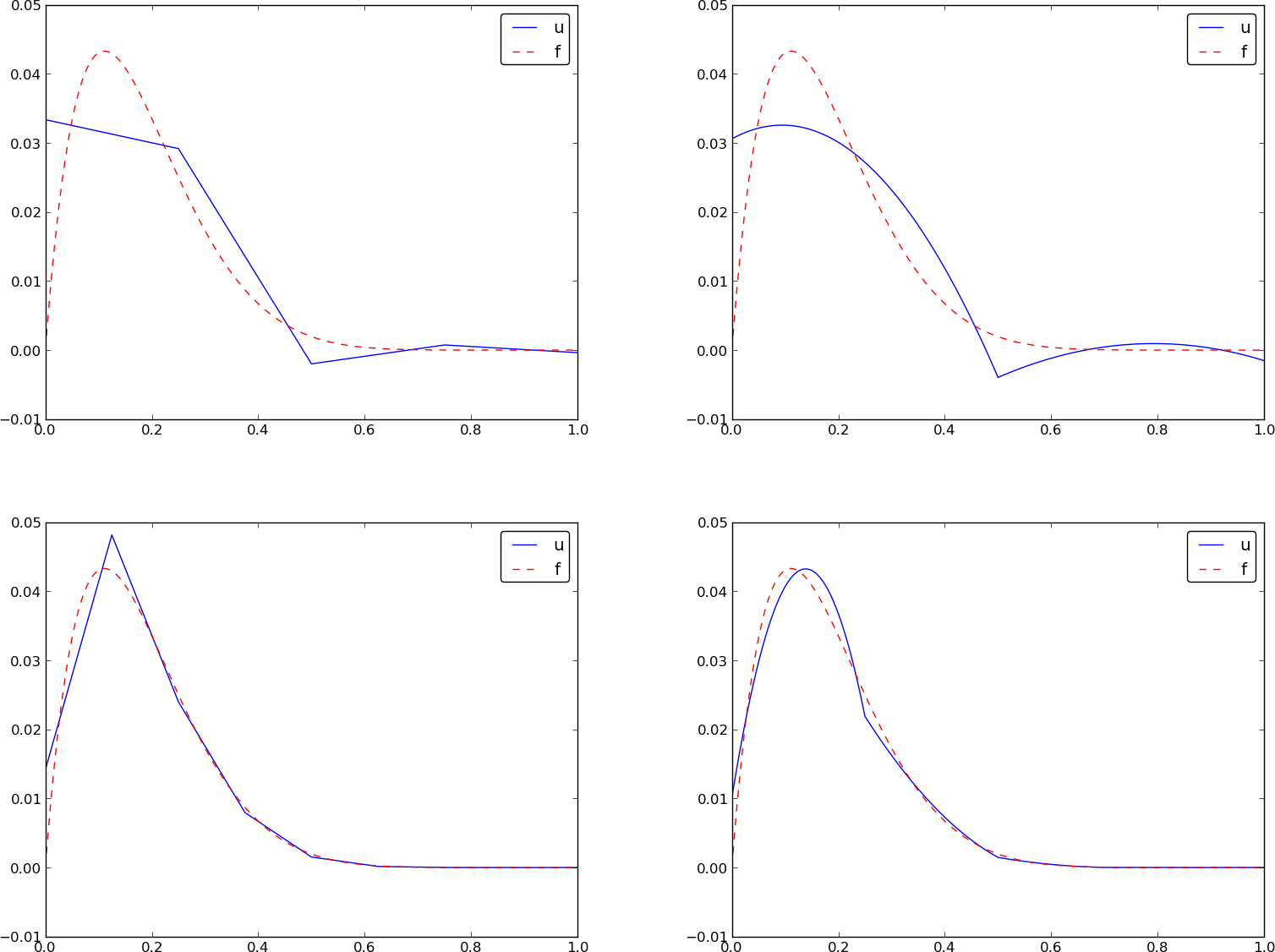
Najczęstsza interpretacja:
wartości \( u \) (wymagane do geometrii i aproksymacji funkcji)
Problem:
– wielkości reprezentowane przez \( c_j \) (niewiadome w URL) -> najczęściej: wartości funkcji w węźle \( \sum_{j\in\If} c_j \basphi_j(\xno{i}) = c_i \)
wierzchołki -> komórki -> interpolacja geometrii
węzły, stopnie swobody -> interpolacja funkcji
vertices, cells, dof_mapvertices (równoważne strukturze nodes dla elementów P1)cells[e][r] numer globalny dla wierchołka r elementu e (równoważne strukturze elements dla elementów typu P1)dof_map[e,r] odwzorowanie lokalnego indeksu stopnia swobody r elementu e na number globalny (równoważne strukturze elements dla elementów typu Pd)
W trakcie assemblingu należy skorzystać ze struktury dof_map:
A[dof_map[e][r], dof_map[e][s]] += A_e[r,s]
b[dof_map[e][r]] += b_e[r]
|
|
vertices = [0, 0.4, 1]
cells = [[0, 1], [1, 2]]
dof_map = [[0, 1, 2], [2, 3, 4]]
|
Przykład: Ta sama siatka, ale \( u \) to funkcja stała na każdej komórce (przedziałami stała) -> elementy typu P0.
Te same struktury vertices i cells, ale dodatkowo
dof_map = [[0], [1]]
Można traktować te elementy jak elementy z interpolacją opartą na węźle znajdującym się pośrodku elementu.
Od tej pory będziemy wykorzystywać struktury cells, vertices, i dof_map.
# Use modified fe_approx1D module
from fe_approx1D_numint import *
x = sym.Symbol('x')
f = x*(1 - x)
N_e = 10
# Create mesh with P3 (cubic) elements
vertices, cells, dof_map = mesh_uniform(N_e, d=3, Omega=[0,1])
# Create basis functions on the mesh
phi = [basis(len(dof_map[e])-1) for e in range(N_e)]
# Create linear system and solve it
A, b = assemble(vertices, cells, dof_map, phi, f)
c = np.linalg.solve(A, b)
# Make very fine mesh and sample u(x) on this mesh for plotting
x_u, u = u_glob(c, vertices, cells, dof_map,
resolution_per_element=51)
plot(x_u, u)
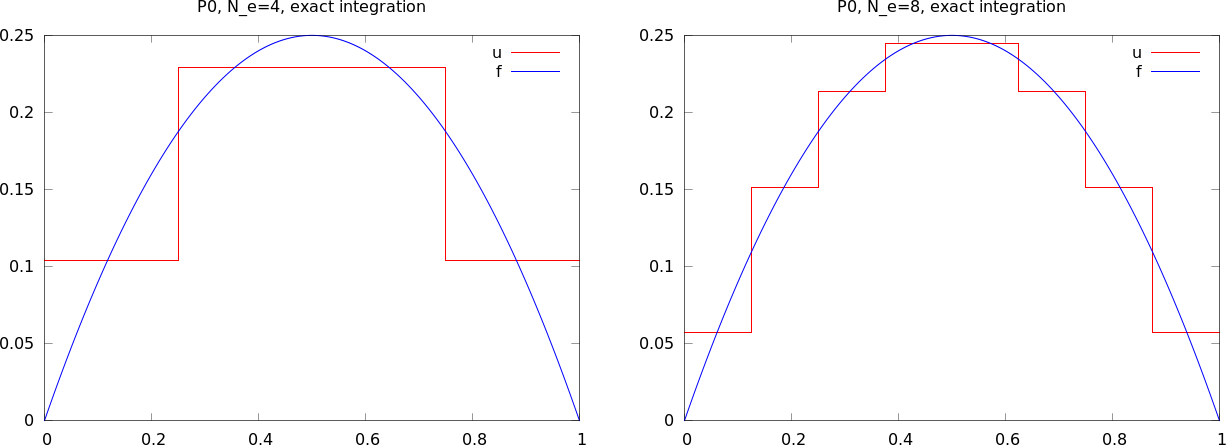
Funkcja approximate ''opakowuje'' polecenia z poprzedniego slajdu:
from fe_approx1D_numint import *
x=sym.Symbol("x")
for N_e in 4, 8:
approximate(x*(1-x), d=0, N_e=N_e, Omega=[0,1])
Błąd jako funkcja:
$$ e(x) = f(x) - u(x) $$
Błąd – dyskretna wartość -> normy:
$$ L^2 \hbox{ error: }\quad ||e||_{L^2} =
\left(\int_{\Omega} e^2 dx\right)^{1/2}$$
Szacowanie całki:
u_glob, które zwróci x i u), a następnie
Ponieważ elementy mogą być różnych rozmiarów (długości) siatka dyskretna może być niejednorodna, (ponadto powtórzone punkty na granicach elementów, widziane z perspektywy dwóch sąsiadujących elementów)
->
potrzebna prymitywna implementacja wzoru trapezów:
$$ \int_\Omega g(x) dx \approx \sum_{j=0}^{n-1} \half(g(x_j) +
g(x_{j+1}))(x_{j+1}-x_j)$$
# Given c, compute x and u values on a very fine mesh
x, u = u_glob(c, vertices, cells, dof_map,
resolution_per_element=101)
# Compute the error on the very fine mesh
e = f(x) - u
e2 = e**2
# Vectorized Trapezoidal rule
E = np.sqrt(0.5*np.sum((e2[:-1] + e2[1:])*(x[1:] - x[:-1]))
Teoria i eksperymenty pokazują, że aplikacja \( \LSM \) czy metody Galerkina dla elementów skończonych typu Pd o tej samej długości \( h \) daje błąd:
$$
||e||_{L^2} = C | f^{d+1} | h^{d+1}
$$
gdzie \( C \) zależy od \( d \) i \( \Omega = [0, L] \) ale nie zależy od \( h \), oraz
$$
|f^{d+1}|^{2} = \int_0^L \left( \frac{d^{d+1}f}{d x^{d+1}} \right)^2 dx
$$
Niech dana będzie unormowana komórka \( [-1,1] \) z dwoma węzłami \( X=-1 \) i \( X=1 \). Stopnie swobody:
Uwzględnienie wartości pochodnych zadanej funkcji w węzłach jako stopni swobody zapewnia kontrolę ciągłości pochodnej.
4 ogranicznia na \( \refphi_r \) (1 dla stopnia swobody \( r \), 0 dla pozostałych):
Cztery układy równań liniowych z 4 niewiadomymi - współczynnikami wielomianów 3 stopnia.
$$
\begin{align}
\refphi_0(X) &= 1 - \frac{3}{4}(X+1)^2 + \frac{1}{4}(X+1)^3
\tag{21}\\
\refphi_1(X) &= -(X+1)(1 - \half(X+1))^2
\tag{22}\\
\refphi_2(X) &= \frac{3}{4}(X+1)^2 - \half(X+1)^3
\tag{23}\\
\refphi_3(X) &= -\half(X+1)(\half(X+1)^2 - (X+1))
\tag{24}\\
\tag{25}
\end{align}
$$
# definition of the interval ends
x = np.array([-1, 1])
C = [] # list of polynomials stored as coefficients
B = [] # list of basis functions
dB = [] # list of the derivatives of basis functions
for k in np.arange(0,4):
A = np.array( [[ x[0]**3, x[0]**2, x[0], 1 ],
[ 3*x[0]**2, 2*x[0], 1, 0 ],
[ x[1]**3, x[1]**2, x[1], 1 ],
[ 3*x[1]**2, 2*x[1], 1, 0 ]])
b = np.zeros( (4,1) ); b[k] = 1
c = np.linalg.solve(A, b); C.append( c )
B.append( lambda x: C[k][0,0] * x**3 + C[k][1,0] * x**2 + C[k][2,0] * x + C[k][3,0] )
dB.append( lambda x: 3* C[k][0,0] * x**2 + 2*C[k][1,0] * x + C[k][2,0] )
# Check numerically that resulting cubic polynomial
# fulfills imposed requirements
A = [1, 1, 2, 1] # basis function coefficients
# U(x[0]) dU(x[0]) U(x[1]) dU(x[1])
xx = np.arange(-1,1, 0.001)
U = np.zeros(xx.shape)
for k in np.arange(0,4):
U = U + A[k] * B[k](xx)
# numerical approximation of the derivatives at the ends of the interval
dl = (U[1]-U[0])/(xx[1]-xx[0])
dr = (U[-1]-U[-2])/(xx[-1]-xx[-2])
numericalApproximationOfA = [ U[0], dl, U[-1], dr]
print(numericalApproximationOfA)
Wynik działania skryptu:
[1.0, 0.9992502500000269, 1.999000749750002, 0.9977517500000526]
|
|
|
$$
\int_{-1}^{1} g(X)dX \approx \sum_{j=0}^M w_jg(\bar X_j),
$$
gdzie
Różne metody -> różny wybór węzłów i wag
(ang. midpoint rule) – metoda punktu środkowego
Najprostsza metoda
$$
\int_{-1}^{1} g(X)dX \approx 2g(0),\quad \bar X_0=0,\ w_0=2,
$$
Dokładna dla funkcji podcałkowych będących wielomianami 1. stopnia
Wzór trapezów:
$$
\int_{-1}^{1} g(X)dX \approx g(-1) + g(1),\quad \bar X_0=-1,\ \bar X_1=1,\ w_0=w_1=1,
$$
Wzór Simpsona (parabol):
$$
\int_{-1}^{1} g(X)dX \approx \frac{1}{3}\left(g(-1) + 4g(0)
+ g(1)\right),
$$
gdzie
$$
\bar X_0=-1,\ \bar X_1=0,\ \bar X_2=1,\ w_0=w_2=\frac{1}{3},\ w_1=\frac{4}{3}
$$
$$
\begin{align}
M=1&:\quad \bar X_0=-\frac{1}{\sqrt{3}},\
\bar X_1=\frac{1}{\sqrt{3}},\ w_0=w_1=1
\tag{26}\\
M=2&:\quad \bar X_0=-\sqrt{\frac{3}{{5}}},\ \bar X_0=0,\
\bar X_2= \sqrt{\frac{3}{{5}}},\ w_0=w_2=\frac{5}{9},\ w_1=\frac{8}{9}
\tag{27}
\end{align}
$$
Plik `numint.py zawiera zbiór węzłów i wag dla metody Gaussa-Legendre'a.
Rozwiązania i algorytmy przedstawione dla aproksymacji funkcji \( f(x) \) w 1D da się rozwinąć i ''przenieść'' na przypadki funkcji \( f(x,y) \) w 2D i \( f(x,y,z) \) w 3D. Ogólne wzory pozostają takie same.
Iloczyn skalarny w 2D:
$$
(f,g) = \int_\Omega f(x,y)g(x,y) dx dy
$$
Zastosowanie \( \LSM \) lub metody Galerkina da URL:
$$
\begin{align*}
\sum_{j\in\If} A_{i,j}c_j &= b_i,\quad i\in\If\\
A_{i,j} &= (\baspsi_i,\baspsi_j)\\
b_i &= (f,\baspsi_i)
\end{align*}
$$
Problem: Jak skonstruować dwuwymiarowe funkcje bazowe \( \baspsi_i(x,y) \)?
Korzystając z funkcji bazowych 1D zmiennej \( x \) oraz funkcji bazowych 1D zmiennej \( y \):
$$
\begin{align}
V_x &= \mbox{span}\{ \hat\baspsi_0(x),\ldots,\hat\baspsi_{N_x}(x)\}
\tag{28}\\
V_y &= \mbox{span}\{ \hat\baspsi_0(y),\ldots,\hat\baspsi_{N_y}(y)\}
\tag{29}
\end{align}
$$
Przestrzeń wektorowa 2D może być zdefinowana jako iloczyn tensorowy \( V = V_x\otimes V_y \) z funkcjami bazowymi:
$$
\baspsi_{p,q}(x,y) = \hat\baspsi_p(x)\hat\baspsi_q(y)
\quad p\in\Ix,q\in\Iy\tp
$$
Niech dane będą dwa wektory \( a=(a_0,\ldots,a_M) \) i \( b=(b_0,\ldots,b_N) \). Ich zewnętrznym iloczynem tensorowym ( iloczynem diadycznym jeśli \( N=M \)) jest \( p=a\otimes b \) zdefiniowane jako:
$$ p_{i,j}=a_ib_j,\quad i=0,\ldots,M,\ j=0,\ldots,N\tp$$
Uwaga: \( p \) to macierz/tablica dwuwymiarowa
Przykład: baza 2D jako iloczyn tensorowy przestrzeni 1D:
$$ \baspsi_{p,q}(x,y) = \hat\baspsi_p(x)\hat\baspsi_q(y),
\quad p\in\Ix,q\in\Iy$$
(dowolnych wymiarów) ->
iloczyn tensorowy wektorów(dowolnych wymiarów) ->
iloczyn diadyczny(tego samego wymiaru)
tensorBaza przestrzeni 2D wymaga dwóch indeksów (i podwójnego sumowania) :
$$ u = \sum_{p\in\Ix}\sum_{q\in\Iy} c_{p,q}\baspsi_{p,q}(x,y)
$$
Lub tylko jednego indeksu
$$ u = \sum_{j\in\If} c_j\baspsi_j(x,y)$$
jeśli posiadamy odwzorowanie \( (p,q)\rightarrow i \):
$$
\baspsi_i(x,y) = \hat\baspsi_p(x)\hat\baspsi_q(y),
\quad i=p (N_y+1) + q\hbox{ or } i=q (N_x+1) + p
$$
Dla dwuelementowej bazy 1D
$$ \{ 1, x \} $$
iloczyn tensorowy (wszystkie kombinacje) generuje bazę przestrzeni 2D:
$$ \baspsi_{0,0}=1,\quad \baspsi_{1,0}=x, \quad \baspsi_{0,1}=y,
\quad \baspsi_{1,1}=xy
$$
W notacji jednoindeksowej:
$$ \baspsi_0=1,\quad \baspsi_1=x, \quad \baspsi_2=y,\quad\baspsi_3 =xy
$$
$$ \baspsi_0=1,\quad \baspsi_1=x, \quad \baspsi_2=y,\quad\baspsi_3 =xy
$$
$$
\int_0^{L_y} \int_0^{L_x}
\left\{
\left[
\begin{array}{cccc}
1\cdot 1 & 1 \cdot x & 1 \cdot y & 1 \cdot xy \\
x\cdot 1 & x \cdot x & x \cdot y & x \cdot xy \\
y\cdot 1 & y \cdot x & y \cdot y & y \cdot xy \\
xy\cdot 1 & xy \cdot x & xy \cdot y & xy \cdot xy
\end{array}
\right]
\left[
\begin{array}{c}
c_0 \\
c_1 \\
c_2 \\
c_3
\end{array}
\right]
=
\left[
\begin{array}{c}
1\cdot f(x,y) \\
x\cdot f(x,y) \\
y\cdot f(x,y) \\
xy\cdot f(x,y)
\end{array}
\right]
\right\}
dxdy
$$
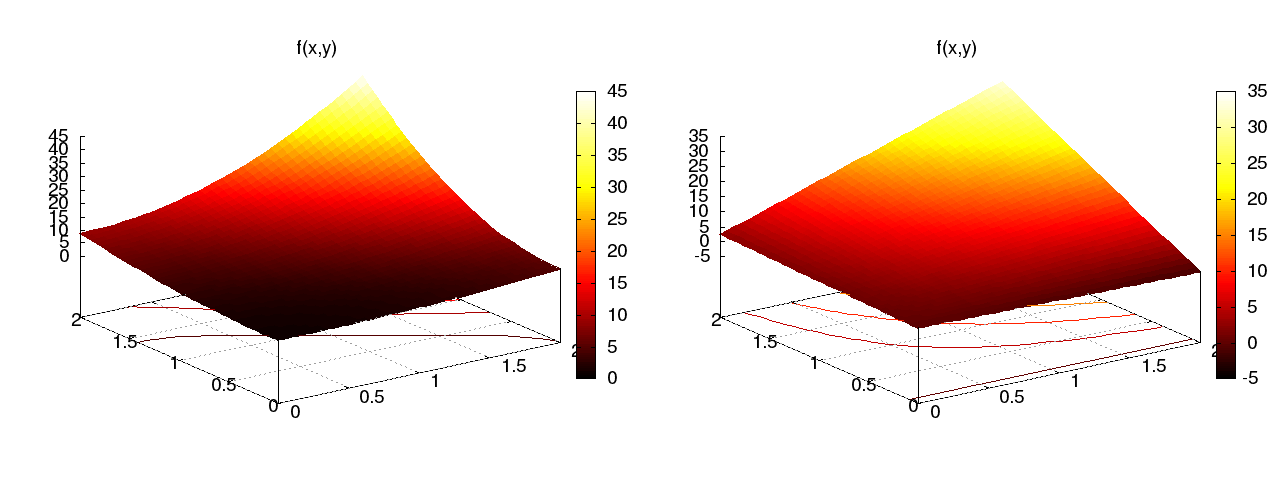
Funkcja aproksymowana (kwadratowa) \( f(x,y) = (1+x^2)(1+2y^2) \) (po lewej), funkcja aproksymująca (biliniowa) \( u \) (po prawej) (\( x^2y^2 \) vs \( xy \)):
Zmiany w kodzie w stosunku do wersji 1D (approx1D.py):
Omega = [[0, L_x], [0, L_y]]import sympy as sym
integrand = psi[i]*psi[j]
I = sym.integrate(integrand,
(x, Omega[0][0], Omega[0][1]),
(y, Omega[1][0], Omega[1][1]))
# Fall back on numerical integration if symbolic integration
# was unsuccessful
if isinstance(I, sym.Integral):
integrand = sym.lambdify([x,y], integrand)
I = sym.mpmath.quad(integrand,
[Omega[0][0], Omega[0][1]],
[Omega[1][0], Omega[1][1]])
Iloczyn tensorowy bazy potęgowej \( x^i \) (bazy Taylora):
def taylor(x, y, Nx, Ny):
return [x**i*y**j for i in range(Nx+1) for j in range(Ny+1)]
Iloczyn tensorowy bazy sinusoidalnej \( \sin((i+1)\pi x) \):
def sines(x, y, Nx, Ny):
return [sym.sin(sym.pi*(i+1)*x)*sym.sin(sym.pi*(j+1)*y)
for i in range(Nx+1) for j in range(Ny+1)]
Cały kod w approx2D.py.
>>> from approx2D import *
>>> f = (1+x**2)*(1+2*y**2)
>>> psi = taylor(x, y, 1, 1)
>>> Omega = [[0, 2], [0, 2]]
>>> u, c = least_squares(f, psi, Omega)
>>> print u
8*x*y - 2*x/3 + 4*y/3 - 1/9
>>> print sym.expand(f)
2*x**2*y**2 + x**2 + 2*y**2 + 1
Dodajemy funkcje bazowe o wyższych potęgach tak, aby \( f\in V \). Spodziewany wynik: \( u=f \)
>>> psi = taylor(x, y, 2, 2)
>>> u, c = least_squares(f, psi, Omega)
>>> print u
2*x**2*y**2 + x**2 + 2*y**2 + 1
>>> print u-f
0
Kluczowa idea:
$$ V = V_x\otimes V_y\otimes V_z$$
$$
\begin{align*}
a^{(q)} &= (a^{(q)}_0,\ldots,a^{(q)}_{N_q}),\quad q=0,\ldots,m\\
p &= a^{(0)}\otimes\cdots\otimes a^{(m)}\\
p_{i_0,i_1,\ldots,i_m} &= a^{(0)}_{i_1}a^{(1)}_{i_1}\cdots a^{(m)}_{i_m}
\end{align*}
$$
W szczególności dla 3D:
$$
\begin{align*}
\baspsi_{p,q,r}(x,y,z) &= \hat\baspsi_p(x)\hat\baspsi_q(y)\hat\baspsi_r(z)\\
u(x,y,z) &= \sum_{p\in\Ix}\sum_{q\in\Iy}\sum_{r\in\Iz} c_{p,q,r}
\baspsi_{p,q,r}(x,y,z)
\end{align*}
$$
Zalety \( \FEM \) w zastosowaniach 2D i 3D:
\( \FEM \) w 1D: głównie dla celów dydaktycznych, debugowania
2D:
3D:
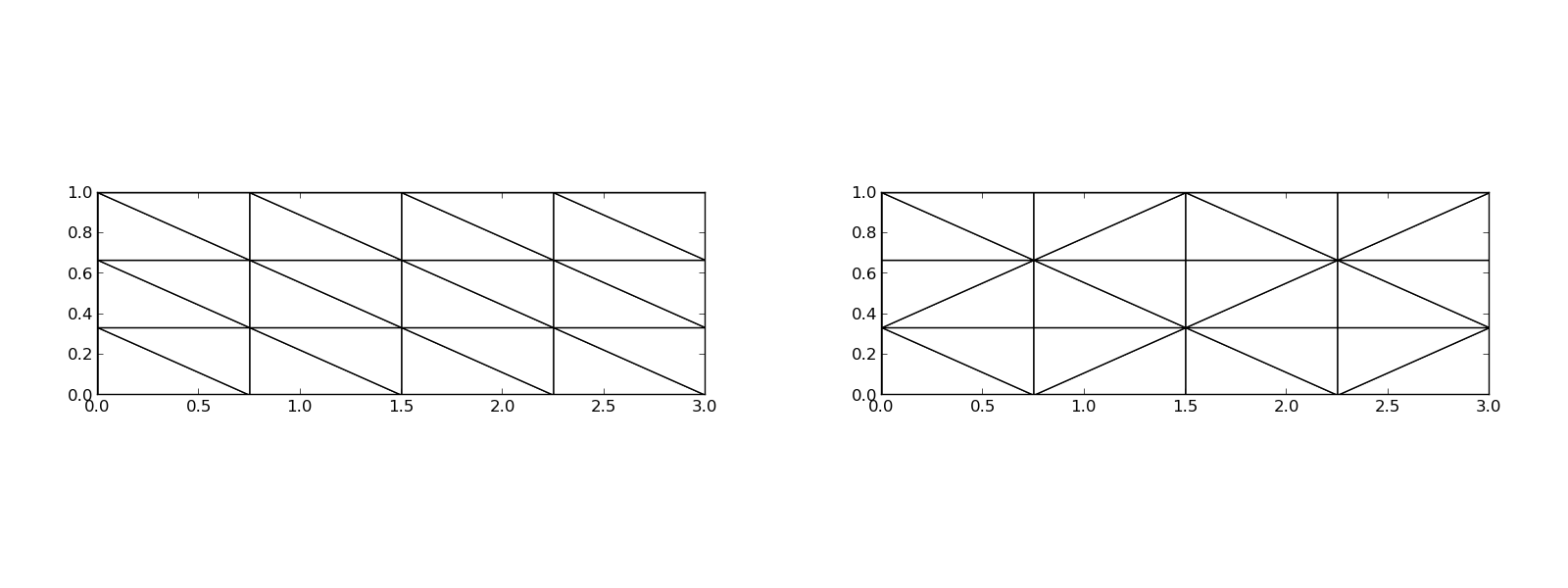
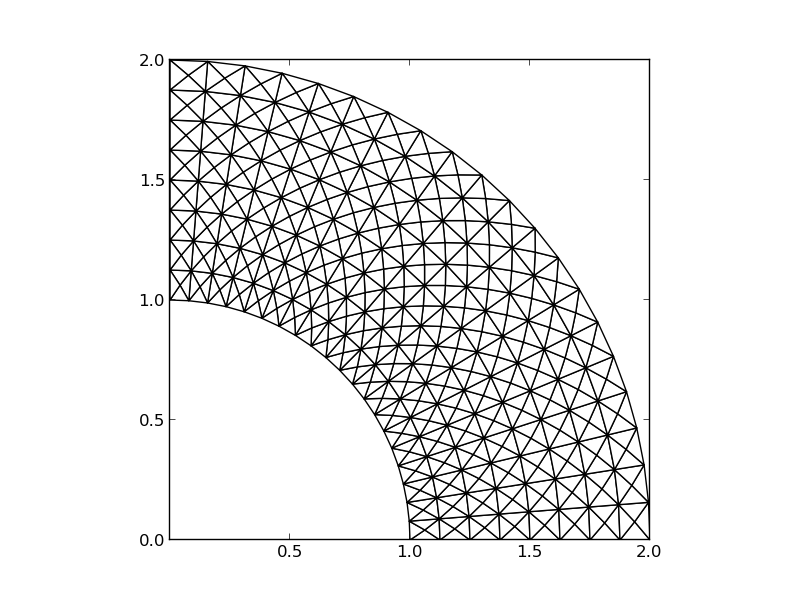
Element trójkątny typu P1: aproksymacja \( u \) na każdym elemencie (komórce) funkcją liniową \( ax + by + c \)


$$
\begin{align}
\refphi_0(X,Y) &= 1 - X - Y
\tag{30}\\
\refphi_1(X,Y) &= X
\tag{31}\\
\refphi_2(X,Y) &= Y
\tag{32}
\end{align}
$$
Funkcje bazowe \( \refphi_r \) wyższych stopni opierają się na większej liczbie węzłów (stopni swobody)



Transformacja (Odwzorowanie) komórki we współrzędnych unormowanych
\( \X = (X,Y) \)do komórki we współrzędnych globalnych:
\( \x = (x,y) \):
$$
\begin{equation}
\x = \sum_{r} \refphi_r^{(1)}(\X)\xdno{q(e,r)}
\tag{33}
\end{equation}
$$
gdzie
Odwzorowanie zachowuje liniowość ścian i krawędzi.

Idea: Wykorzystanie funkcji bazowych elementu (nie tylko funkcji typu P1 ale i wyższych rzędów) do odwzorowania geometrii:
$$
\x = \sum_{r} \refphi_r(\X)\xdno{q(e,r)}
$$
Zaleta: pozwala generować elementy o geomtrii nielinowej

Wymagana transformacja całek z \( \Omega^{(e)} \) (komórka we współrządnych globalnych) w \( \tilde\Omega^r \) (komórka unormowana/odniesienia):
$$
\begin{align}
\int_{\Omega^{(e)}}\basphi_i (\x) \basphi_j (\x) \dx &=
\int_{\tilde\Omega^r} \refphi_i (\X) \refphi_j (\X)
\det J\, \dX
\tag{34}\\
\int_{\Omega^{(e)}}\basphi_i (\x) f(\x) \dx &=
\int_{\tilde\Omega^r} \refphi_i (\X) f(\x(\X)) \det J\, \dX
\tag{35}
\end{align}
$$
gdzie \( \dx = dx dy \) lub \( \dx = dxdydz \) oraz \( \det J \) to wyznacznik jakobianu odwzorowania \( \x(\X) \).
$$
J = \left[\begin{array}{cc}
\frac{\partial x}{\partial X} & \frac{\partial x}{\partial Y}\\
\frac{\partial y}{\partial X} & \frac{\partial y}{\partial Y}
\end{array}\right], \quad
\det J = \frac{\partial x}{\partial X}\frac{\partial y}{\partial Y}
- \frac{\partial x}{\partial Y}\frac{\partial y}{\partial X}
$$
Odwzorowanie afiniczne (33): \( \det J=2\Delta \), \( \Delta = \hbox{powierzchnia komórki/elementu} \)
Ogólna idea \( \FEM \) oraz kroki algorytmu – takie same niezależnie od wymiarowości geometrii.
Im wyższy wymiar przestrzeni, tym większy nakład obliczeniowy. ze względu na komplikację wzorów.
Obliczenia ręczne - nużące, podatne na popełnienie pomyłki.
Automatyzacja i algorytmizacja problemu pożądana.
/