Figure 1

Finite Element Method, FEM, MES
Figure 1

Figure 2

Figure 3

Istnieje wiele wariantów i odmian \( \FEM \). Dzięki proponowanemu podejściu łatwiej się ''połapać''. Unikamy zamieszania wielością podejść do tematu, koncepcji i technicznych/implementacyjnych szczegółów.
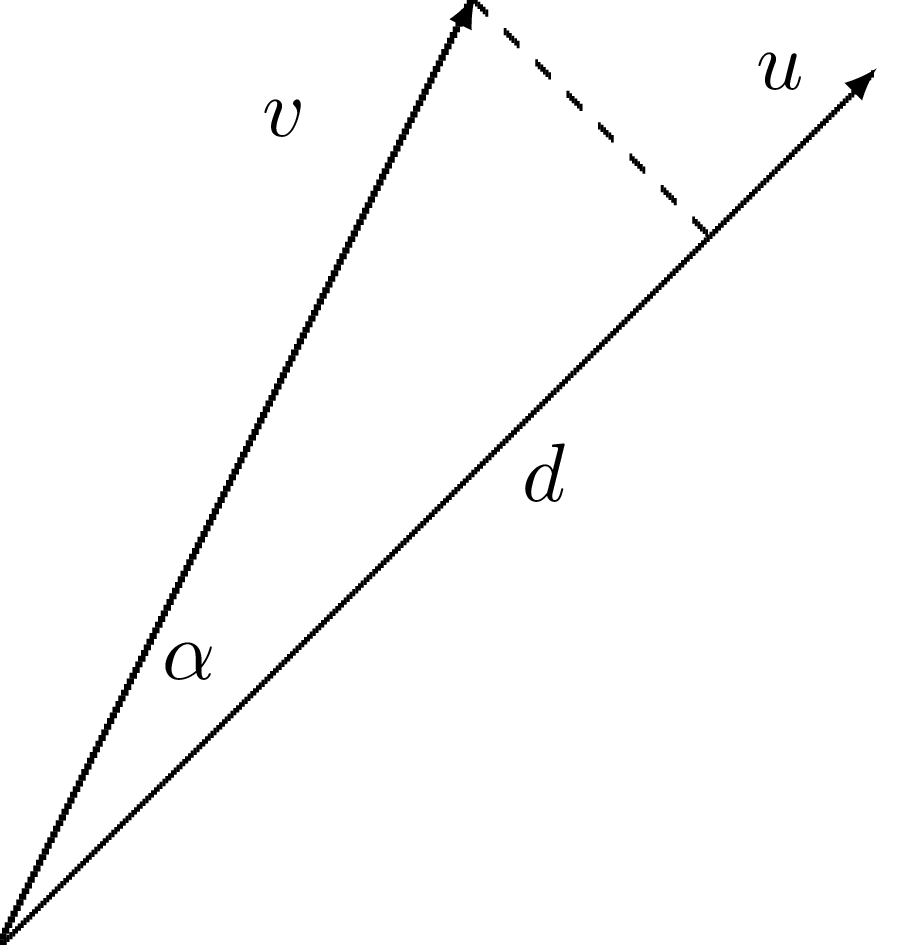
Jak znaleźć wektor pewnej przestrzeni, który aproksymuje wektor przestrzeni o większym wymiarze?
Figure 4
Ogólna idea poszukiwania elementu (wektora/funkcji) \( u(x) \) pewnej przestrzeni przybliżającego zadany element \( f(x) \):
$$ u(x) = \sum_{i=0}^N c_I \baspsi_i(x) $$gdzie
Sposób opisu i notacja zaproponowane w materiałach pozwalają na (nieco) łatwiejsze rozpoczęcie pracy i zrozumienie zasady działania wybrane w sposób ułatwiający zrozumienie open-source'owego pakietu FEniCS – biblioteki do obliczeń metodą elementów skończonych.
Zadanie:
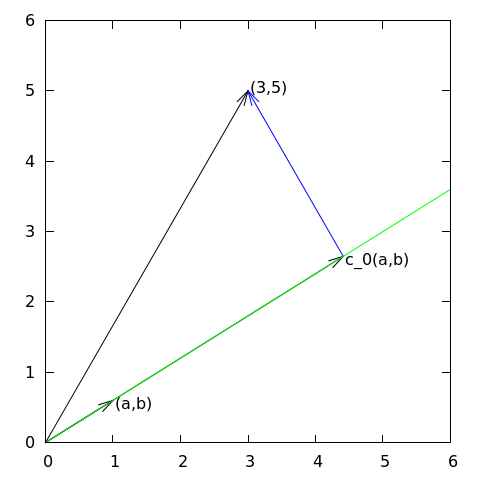
Znajdź przybliżenie wektora \( \f = (3,5) \) wzdłuż zadanego kierunku.
Figure 5

analogie: element - punkt - wektor - funkcja
Figure 6
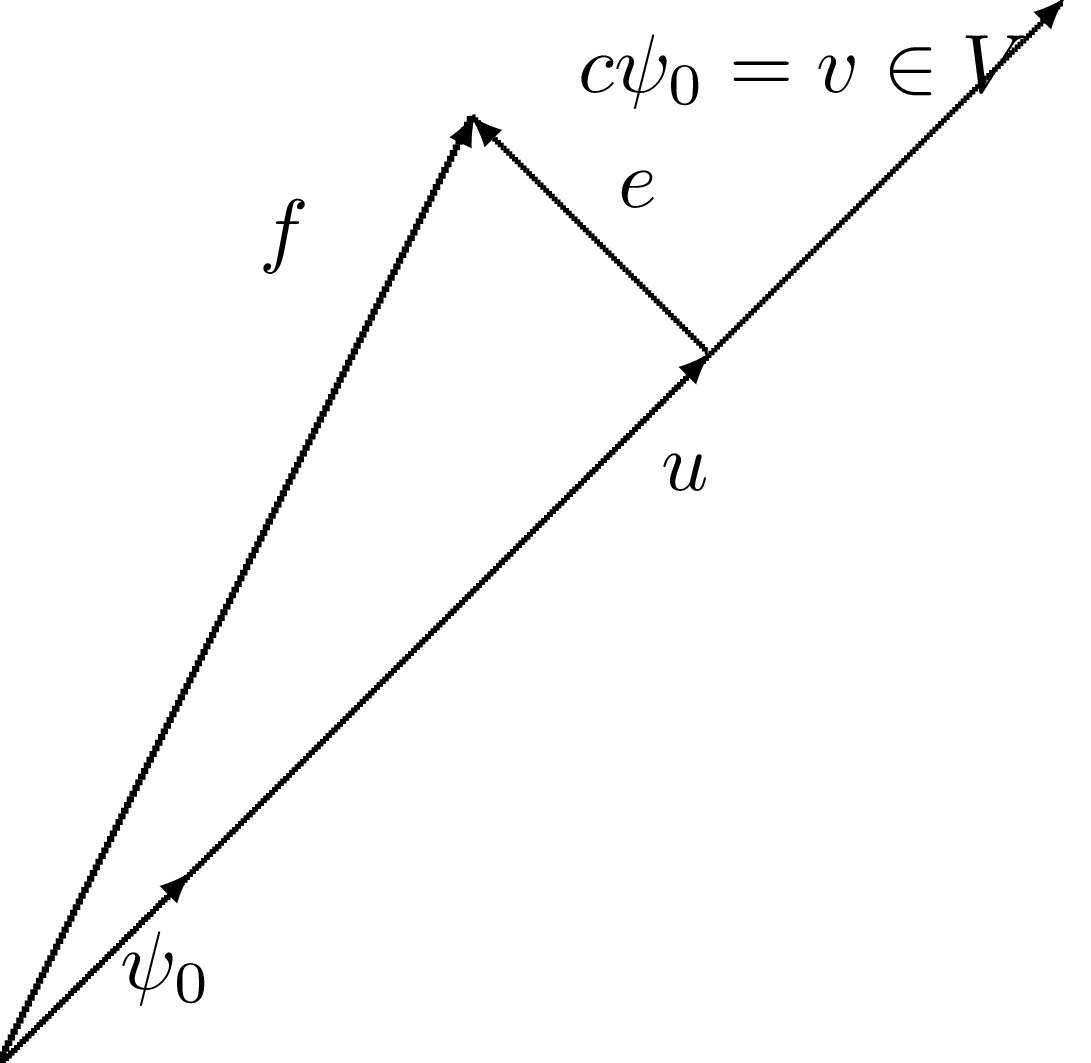
Niech
\( (a,b) \) – punkt/wektor przestrzeni (dwuwymiarowej)
\( (\u,\v) \) – iloczyn skalarny dwóch wektorów przestrzeni (dowolnie-wymiarowej)
Spostrzeżenie (na później): warunek znikania pochodnej \eqref{fem:vec:dEdc0:v1} można równoważnie zapisać jako:
$$ (\e, \psib_0) = 0 $$ $$ (\e, \psib_0) = (\f - \u, \psib_0) = (\f, \psib_0) - (\u, \psib_0) .... \quad\quad (*-2 ...) $$ $$ [\f-\u] \cdot \left[ \begin{array}{c} \\ \psib_0 \\ \\ \end{array} \right] = [\quad\quad \f \quad\quad] \cdot \left[ \begin{array}{c} \\ \psib_0 \\ \\ \end{array} \right] - [\quad\quad \u \quad\quad] \cdot \left[ \begin{array}{c} \\ \psib_0 \\ \\ \end{array} \right] $$Figure 7
Dla danego wektora \( \f \), znajdź przybliżenie \( \u\in V \):
$$ \begin{equation*} V = \hbox{span}\,\{\psib_0,\ldots,\psib_N\} \end{equation*} $$(\( \hbox{span} \) czyt. przestrzeń rozpięta na wektorach...)
Mając dany zbiór wektorów niezależnych liniowo \( \psib_0,\ldots,\psib_N \), dowolny wektor \( \u\in V \) można zapisać jako:
$$ \u = \sum_{j=0}^Nc_j\psib_j$$
Wykazać, że przy pomocy kombinacji liniowej pewnych 3 wektorów przestrzeni 3D można skonstruować dowolny wektor tej przestrzeni.
Idea: znaleźć takie \( c_0,\ldots,c_N \), aby \( E= ||\e||^2 \) był minimalizowany, \( \e=\f-\u \).
$$ \begin{align*} E(c_0,\ldots,c_N) &= (\e,\e) = (\f -\sum_jc_j\psib_j,\f -\sum_jc_j\psib_j) \nonumber\\ &= (\f,\f) - 2\sum_{j=0}^Nc_j(\f,\psib_j) + \sum_{p=0}^N\sum_{q=0}^N c_pc_q(\psib_p,\psib_q) \end{align*} $$ $$ \begin{equation*} \frac{\partial E}{\partial c_i} = 0,\quad i=0,\ldots,N \end{equation*} $$Po odrobinie obliczeń otrzymuje się układ równań liniowych:
$$ \begin{align} \sum_{j=0}^N A_{i,j}c_j &= b_i,\quad i=0,\ldots,N \label{_auto1}\\ A_{i,j} &= (\psib_i,\psib_j) \label{_auto2}\\ b_i &= (\psib_i, \f) \label{_auto3} \end{align} $$Można pokazać, że poszukiwanie minimalnego \( ||\e|| \) jest równoważne poszukiwaniu \( \e \) ortogonalnego do wszystkich \( \v\in V \):
$$ (\e,\v)=0,\quad \forall\v\in V $$co jest równoważne temu aby \( \e \) był ortogonalny do każdego wektora bazowego:
$$ (\e,\psib_i)=0,\quad i=0,\ldots,N $$Warunek ortogonalności – podstawa metody Galerkina. Generuje ten sam układ równań liniowych co \( \LSM \).
Niech \( V \) będzie przestrzenią funkcyjną rozpiętą na zbiorze funkcji bazowych \( \baspsi_0,\ldots,\baspsi_N \),
$$ \begin{equation*} V = \hbox{span}\,\{\baspsi_0,\ldots,\baspsi_N\} \end{equation*} $$Dowolną funkcję tej przestrzeni \( u\in V \) można przedstawić jako kombinację liniową funkcji bazowych:
$$ u = \sum_{j\in\If} c_j\baspsi_j,\quad\If = \{0,1,\ldots,N\} $$Tak jak dla przestrzeni wektorowych, minimalizujemy normę błędu \( E \), ze względu na współczynniki \( c_j \), \( j\in\If \):
$$ E = (e,e) = (f-u,f-u) = \left(f(x)-\sum_{j\in\If} c_j\baspsi_j(x), f(x)-\sum_{j\in\If} c_j\baspsi_j(x)\right) $$ $$ \frac{\partial E}{\partial c_i} = 0,\quad i=\in\If $$Czym jest iloczyn skalarny jeśli \( \baspsi_i \) jest funkcją?
$$(f,g) = \int_\Omega f(x)g(x)\, dx$$(iloczyn skalarny funkcji cg jako uogólnienie il. skalarnego funkcji dyskretnych \( (\u, \v) = \sum_j u_jv_j \))
Obliczenia identyczne jak dla przypadku wektorowego -> w rezultacie otrzymujemy układ równań liniowych
$$ \sum_{j\in\If}^N A_{i,j}c_j = b_i,\ i\in\If,\quad A_{i,j} = (\baspsi_i,\baspsi_j),\ b_i = (f,\baspsi_i) $$Jak poprzednio minimalizacja \( (e,e) \) jest równoważna
$$ (e,\baspsi_i)=0,\quad i\in\If \label{fem:approx:Galerkin0} $$co z kolei jest równoważne
$$ (e,v)=0,\quad\forall v\in V \label{fem:approx:Galerkin} $$Równoważność wzorów jak dla przestrzeni wektorowych.
Równoważność wzorów jak dla wyprowadzenia przy pomocy \( \LSM \).
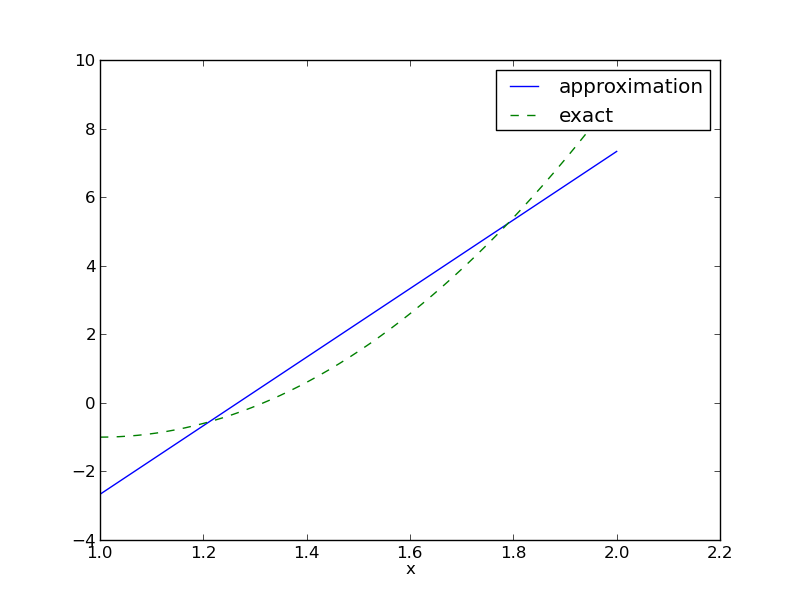
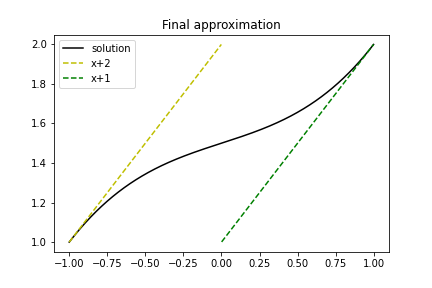
Dla zadanej funkcji \( f(x) = 10(x-1)^2 - 1 \) znaleźć jej przybliżenie funkcją liniową.
czyli \( \baspsi_0(x)=1 \), \( \baspsi_1(x)=x \) oraz \( N=1 \). Szukane
$$ \begin{equation*} u=c_0\baspsi_0(x) + c_1\baspsi_1(x) = c_0 + c_1x \end{equation*} $$Rozwiązanie układu równań 2x2:
$$ c_0 = -38/3,\quad c_1 = 10,\quad u(x) = 10x - \frac{38}{3} $$Figure 8
Problem: napisać program/funkcję, który przeprowadzi obliczenia (obliczenie całek i rozwiązanie układu równań liniowych) i zwróci rozwiązanie postaci n \( u(x)=\sum_jc_j\baspsi_j(x) \).
Niech
sympy oznaczoną symbolem f (funkcję zmiennej (symbolu) x)psi będzie listą funkcji \( \sequencei{\baspsi} \),Omega będzie dwuelementową krotką/listą zawierającą początek i koniec przedziału \( \Omega \)import sympy as sym
def least_squares(f, psi, Omega):
N = len(psi) - 1
A = sym.zeros((N+1, N+1))
b = sym.zeros((N+1, 1))
x = sym.Symbol('x')
for i in range(N+1):
for j in range(i, N+1):
A[i,j] = sym.integrate(psi[i]*psi[j],
(x, Omega[0], Omega[1]))
A[j,i] = A[i,j]
b[i,0] = sym.integrate(psi[i]*f, (x, Omega[0], Omega[1]))
c = A.LUsolve(b)
u = 0
for i in range(len(psi)):
u += c[i,0]*psi[i]
return u, c
Spostrzeżenie: macierz układu jest symetryczna, dzięki czemu można zoptymalizować proces wyznaczania jej elementów
f) , sym.integrate zwróci wtedy obiekt typu sym.Integral. Ulepszenie kodu: sprawdzenie czy takie zdarzenie wystąpiło i ew. obliczenia numeryczne.def least_squares(f, psi, Omega, symbolic=True):
...
for i in range(N+1):
for j in range(i, N+1):
integrand = psi[i]*psi[j]
if symbolic:
I = sym.integrate(integrand, (x, Omega[0], Omega[1]))
if not symbolic or isinstance(I, sym.Integral):
# Could not integrate symbolically,
# fall back on numerical integration
integrand = sym.lambdify([x], integrand)
I = sym.mpmath.quad(integrand, [Omega[0], Omega[1]])
A[i,j] = A[j,i] = I
integrand = psi[i]*f
if symbolic:
I = sym.integrate(integrand, (x, Omega[0], Omega[1]))
if not symbolic or isinstance(I, sym.Integral):
integrand = sym.lambdify([x], integrand)
I = sym.mpmath.quad(integrand, [Omega[0], Omega[1]])
b[i,0] = I
...
Graficzne porównanie \( f \) i \( u \):
def comparison_plot(f, u, Omega, filename='tmp.pdf'):
x = sym.Symbol('x')
# Turn f and u to ordinary Python functions
f = sym.lambdify([x], f, modules="numpy")
u = sym.lambdify([x], u, modules="numpy")
resolution = 401 # no of points in plot
xcoor = linspace(Omega[0], Omega[1], resolution)
exact = f(xcoor)
approx = u(xcoor)
plot(xcoor, approx)
hold('on')
plot(xcoor, exact)
legend(['approximation', 'exact'])
savefig(filename)
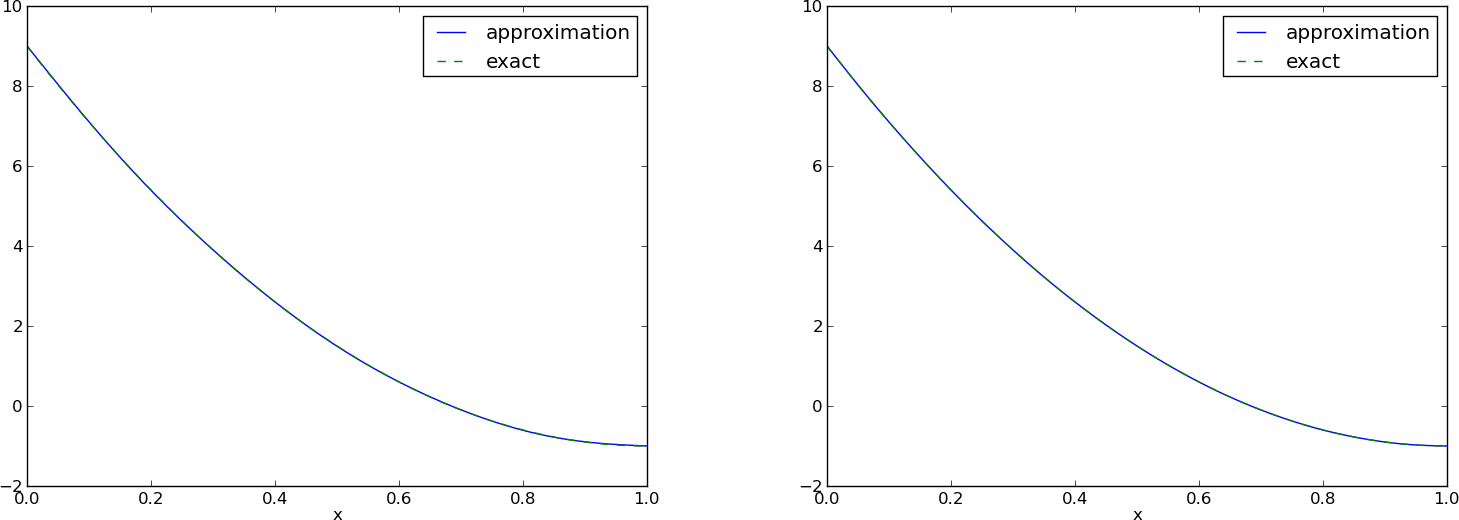
>>> from approx1D import *
>>> x = sym.Symbol('x')
>>> f = 10*(x-1)**2-1
>>> u, c = least_squares(f=f, psi=[1, x], Omega=[1, 2])
>>> comparison_plot(f, u, Omega=[1, 2])
Figure 9

>>> from approx1D import *
>>> x = sym.Symbol('x')
>>> f = 10*(x-1)**2-1
>>> u, c = least_squares(f=f, psi=[1, x, x**2], Omega=[1, 2])
>>> print u
10*x**2 - 20*x + 9
>>> print sym.expand(f)
10*x**2 - 20*x + 9
Rozwiązanie przybliżone \( \equiv \) rozwiązanie dokładne, jeśli \( f \in V \)!
least_squares: dla \( i>2 \), \( c_i=0 \)
Jeśli \( f\in V \), \( \LSM \) oraz metoda Galerkina zwrócą \( u=f \).
Jeśli \( f\in V \), wtedy \( f=\sum_{j\in\If}d_j\baspsi_j \), dla pewnego \( \sequencei{d} \). Wtedy
$$ \begin{equation*} b_i = (f,\baspsi_i) = \sum_{j\in\If}d_j(\baspsi_j, \baspsi_i) = \sum_{j\in\If} d_jA_{i,j} \end{equation*} $$a URL \( \sum_j A_{i,j}c_j = b_i \), \( i\in\If \), przedstawia sie:
$$ \begin{equation*} \sum_{j\in\If}c_jA_{i,j} = \sum_{j\in\If}d_jA_{i,j},\quad i\in\If \end{equation*} $$co oznacza, że \( c_i=d_i \) dla \( i\in\If \), czyli \( u \) jest tożsame z \( f \).
Poprzednie wnioski -> teoria i obliczenia symboliczne \ldots
Co w przypadku obliczeń numerycznych? -> (rozwiązanie URL macierzami liczb zmiennoprzecinkowych)
\( f \) to wciąż funkcja kwadratowa przybliżana przez
$$ u(x) = c_0 + c_1x + c_2x^2 + c_3x^3 +\cdots + c_Nx^N $$Oczekiwane: \( c_2=c_3=\cdots=c_N=0 \), skoro \( f\in V \) oznacza \( u=f \).
A naprawdę?
| teoria | sympy | numpy32 | numpy64 |
|---|---|---|---|
| 9 | 9.62 | 5.57 | 8.98 |
| -20 | -23.39 | -7.65 | -19.93 |
| 10 | 17.74 | -4.50 | 9.96 |
| 0 | -9.19 | 4.13 | -0.26 |
| 0 | 5.25 | 2.99 | 0.72 |
| 0 | 0.18 | -1.21 | -0.93 |
| 0 | -2.48 | -0.41 | 0.73 |
| 0 | 1.81 | -0.013 | -0.36 |
| 0 | -0.66 | 0.08 | 0.11 |
| 0 | 0.12 | 0.04 | -0.02 |
| 0 | -0.001 | -0.02 | 0.002 |
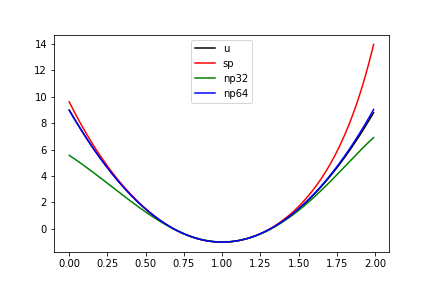
matrix oraz lu_solve z biblioteki sympy.mpmath.fpnumpy 4B liczby zmiennoprzecinkowenumpy 8B liczby zmiennoprzecinkoweŹródło kłopotów: funkcje \( x^i \) dla bardzo dużych \( i \) stają się praktycznie liniowo zależne
4 rozwiązania zadania przybliżenia paraboli
Figure 10
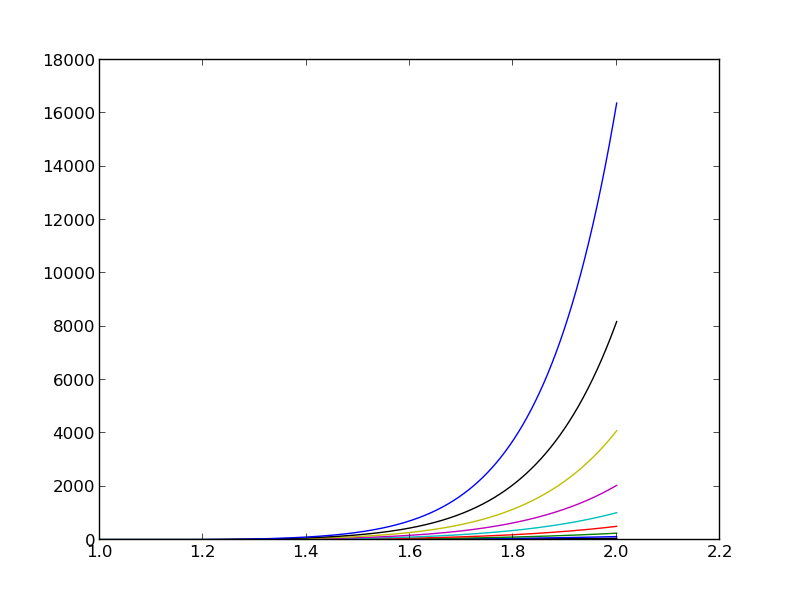
Wykresy funkcji \( x^i \) dla \( i=0 \ldots 14 \)
Figure 11
Aproksymacja funkcji \( f \) szeregiem Fouriera
$$ u(x) = \sum_i a_i\sin i\pi x = \sum_{j=0}^Nc_j\sin((j+1)\pi x) $$to tylko ''zmiana bazy'':
$$ \begin{equation*} V = \hbox{span}\,\{ \sin \pi x, \sin 2\pi x,\ldots,\sin (N+1)\pi x\} \end{equation*} $$Obliczenia z wykorzystaniem funkcji least_squares:
N = 3
from sympy import sin, pi
psi = [sin(pi*(i+1)*x) for i in range(N+1)]
f = 10*(x-1)**2 - 1
Omega = [0, 1]
u, c = least_squares(f, psi, Omega)
comparison_plot(f, u, Omega)
L: \( N=3 \), P: \( N=11 \):
Figure 12
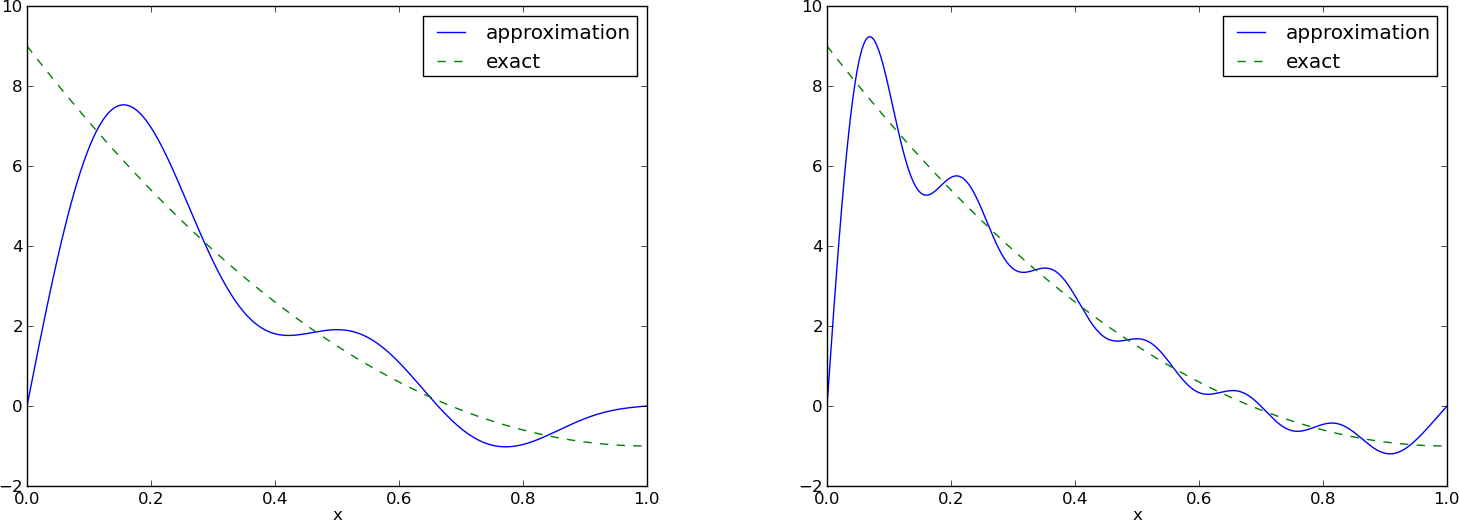
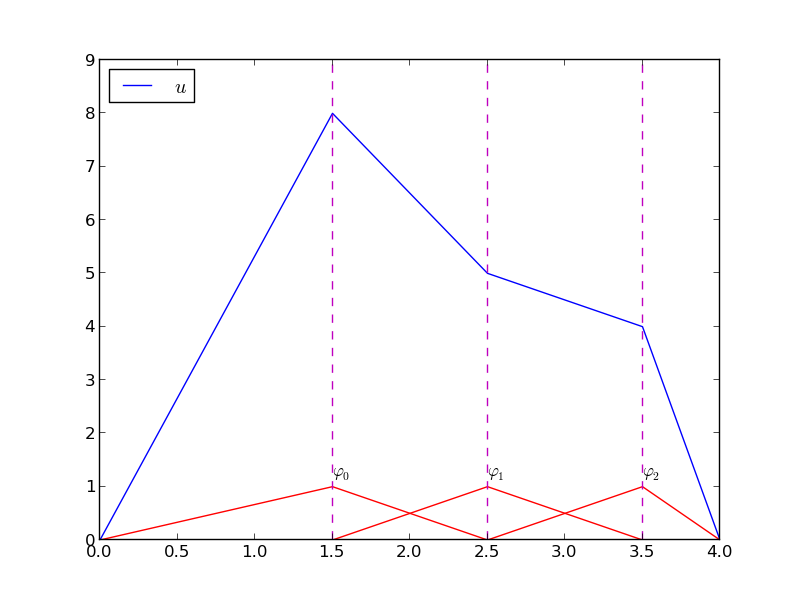
Dla każdej f.bazowej jest \( \baspsi_i(0)=0 \) przez co \( u(0)=0 \neq f(0)=9 \). Podobna sytuacja dla \( x=1 \). Wartości \( u \) na brzegach będą zawsze niepoprawne!
Dodatkowy wyraz nie tylko zapewnia \( u(0)=f(0) \) oraz \( u(1)=f(1) \), ale także zaskakująco dobrze poprawia jakość aproksymacji!
\( N=3 \) vs \( N=11 \):
Figure 13
Zalety wyboru funkcji sinus jako funkcji bazowych:
W ogólnym przypadku, dla baz ortogonalnych, \( A_{i,j} \) jest macierzą diagonalną, a nieznane współczynniki \( c_i \) można łatwo obliczyć:
$$ c_i = \frac{b_i}{A_{i,i}} = \frac{(f,\baspsi_i)}{(\baspsi_i,\baspsi_i)} $$def least_squares_orth(f, psi, Omega):
N = len(psi) - 1
A = [0]*(N+1)
b = [0]*(N+1)
x = sym.Symbol('x')
for i in range(N+1):
A[i] = sym.integrate(psi[i]**2, (x, Omega[0], Omega[1]))
b[i] = sym.integrate(psi[i]*f, (x, Omega[0], Omega[1]))
c = [b[i]/A[i] for i in range(len(b))]
u = 0
for i in range(len(psi)):
u += c[i]*psi[i]
return u, c
symbolic).sym.integrate zwraca sym.Integral), obliczenia wykonywane numerycznie (w przypadku funkcji sinus nie powinno być problemów z symbolicznym obliczeniem \( \int_\Omega\basphi_i^2dx \))def least_squares_orth(f, psi, Omega, symbolic=True):
...
for i in range(N+1):
# Diagonal matrix term
A[i] = sym.integrate(psi[i]**2, (x, Omega[0], Omega[1]))
# Right-hand side term
integrand = psi[i]*f
if symbolic:
I = sym.integrate(integrand, (x, Omega[0], Omega[1]))
if not symbolic or isinstance(I, sym.Integral):
print 'numerical integration of', integrand
integrand = sym.lambdify([x], integrand)
I = sym.mpmath.quad(integrand, [Omega[0], Omega[1]])
b[i] = I
...
Inny sposób znalezienia przybliżenia \( f(x) \) przez \( u(x)=\sum_jc_j\baspsi_j \):
Współczynniki wygenerowanego układu równań to po prostu wartości funkcji, nie ma potrzeby całkowania!
$$ \begin{align} \sum_{j\in\If} A_{i,j}c_j &= b_i,\quad i\in\If \label{_auto4}\\ A_{i,j} &= \baspsi_j(\xno{i}) \label{_auto5}\\ b_i &= f(\xno{i}) \label{_auto6} \end{align} $$W ogólnym przypadku macierz wynikowa niesymetryczna: \( \baspsi_j(\xno{i})\neq \baspsi_i(\xno{j}) \)
Zmienna points przechowuje punkty kolokacji
def interpolation(f, psi, points):
N = len(psi) - 1
A = sym.zeros((N+1, N+1))
b = sym.zeros((N+1, 1))
x = sym.Symbol('x')
# Turn psi and f into Python functions
psi = [sym.lambdify([x], psi[i]) for i in range(N+1)]
f = sym.lambdify([x], f)
for i in range(N+1):
for j in range(N+1):
A[i,j] = psi[j](points[i])
b[i,0] = f(points[i])
c = A.LUsolve(b)
u = 0
for i in range(len(psi)):
u += c[i,0]*psi[i](x)
return u
\( (4/3,5/3) \) vs \( (1,2) \):
Figure 14
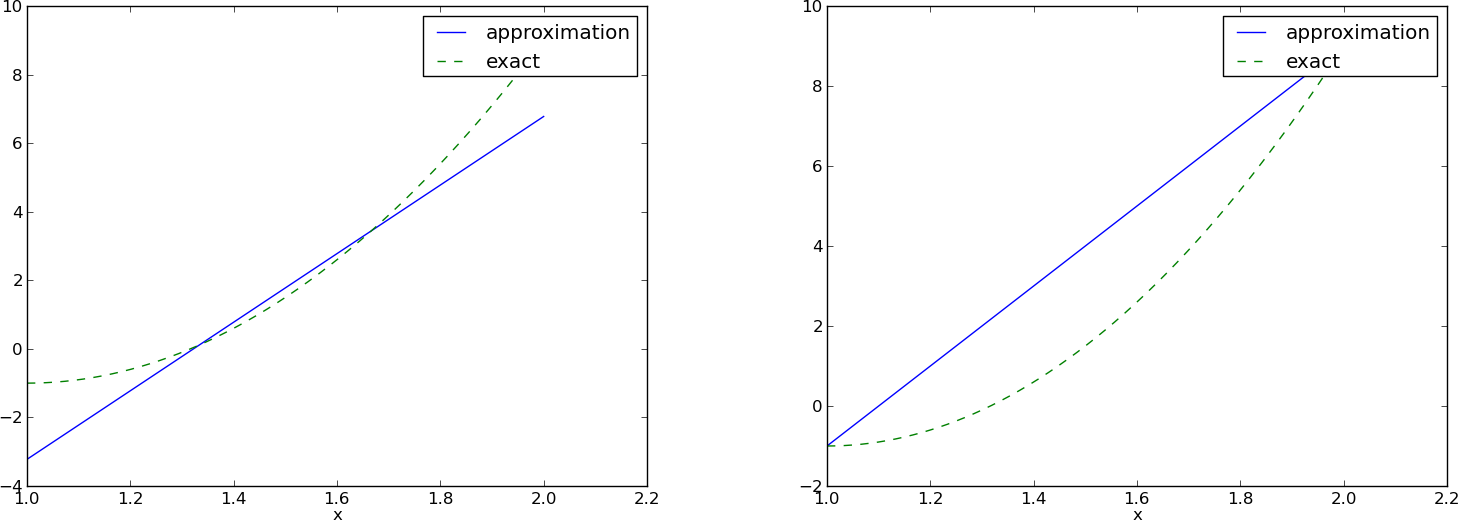
Figure 15

def regression(f, psi, points):
N = len(psi) - 1
m = len(points)
# Use numpy arrays and numerical computing
B = np.zeros((N+1, N+1))
d = np.zeros(N+1)
# Wrap psi and f in Python functions rather than expressions
# so that we can evaluate psi at points[i]
x = sym.Symbol('x')
psi_sym = psi # save symbolic expression
psi = [sym.lambdify([x], psi[i]) for i in range(N+1)]
f = sym.lambdify([x], f)
for i in range(N+1):
for j in range(N+1):
B[i,j] = 0
for k in range(m+1):
B[i,j] += psi[i](points[k])*psi[j](points[k])
d[i] = 0
for k in range(m+1):
d[i] += psi[i](points[k])*f(points[k])
c = np.linalg.solve(B, d)
u = sum(c[i]*psi_sym[i] for i in range(N+1))
return u, c
import sympy as sym
x = sym.Symbol('x')
f = 10*(x-1)**2 - 1
psi = [1, x]
Omega = [1, 2]
m_values = [2-1, 8-1, 64-1]
# Create m+3 points and use the inner m+1 points
for m in m_values:
points = np.linspace(Omega[0], Omega[1], m+3)[1:-1]
u, c = regression(f, psi, points)
comparison_plot(f, u, Omega, points=points,
points_legend='%d interpolation points' % (m+1))
Figure 16

Motywacja::
Własność wielomianów Lagrange'a \( \baspsi_j \):
$$ \baspsi_i(\xno{j}) =\delta_{ij},\quad \delta_{ij} = \left\lbrace\begin{array}{ll} 1, & i=j\\ 0, & i\neq j \end{array}\right. $$Zatem, \( c_i = f(x_i) \) and
$$ u(x) = \sum_{j\in\If} f(\xno{i})\baspsi_i(x) $$def Lagrange_polynomial(x, i, points):
p = 1
for k in range(len(points)):
if k != i:
p *= (x - points[k])/(points[i] - points[k])
return p
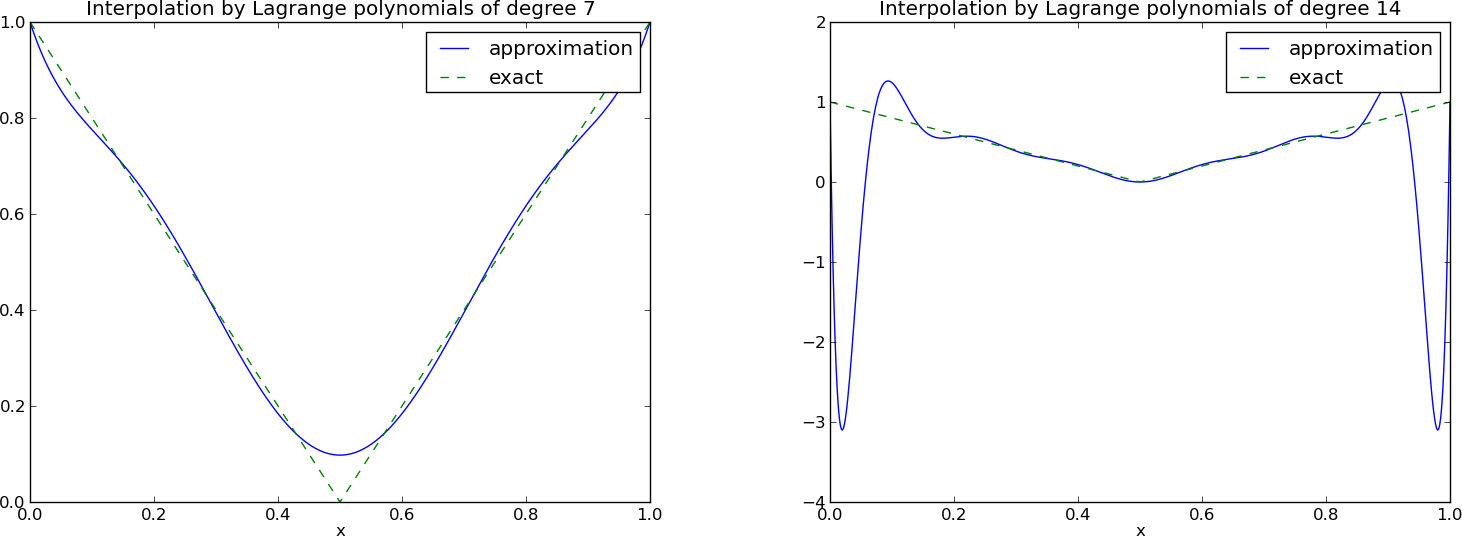
Figure 17
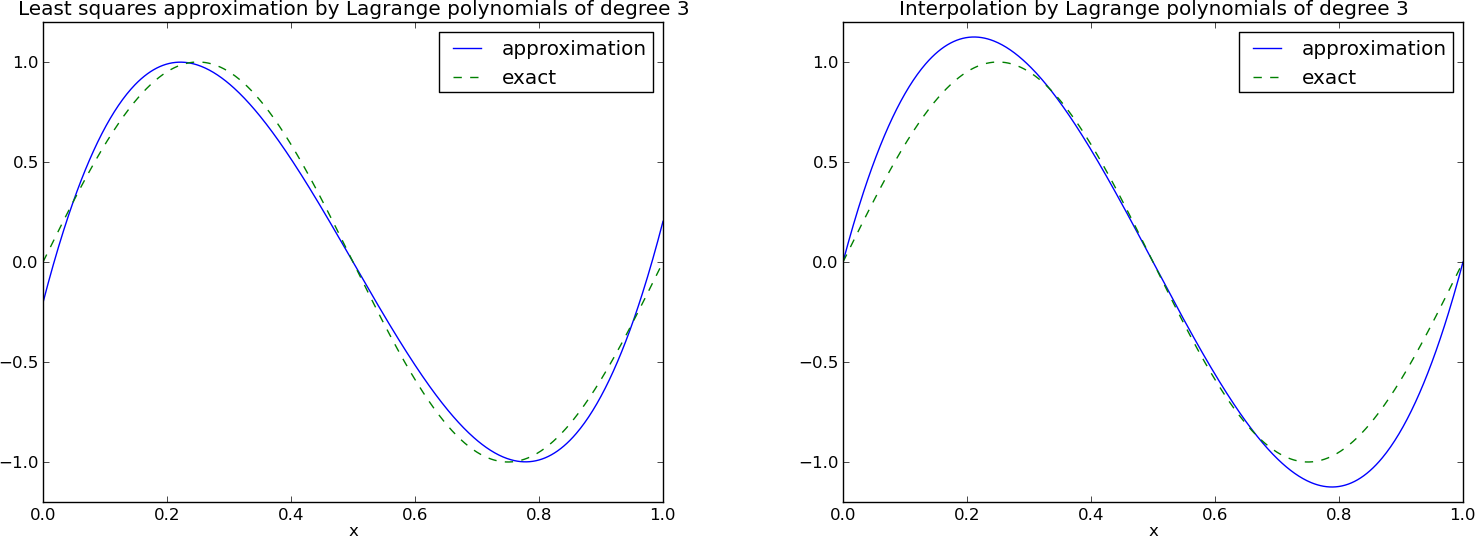
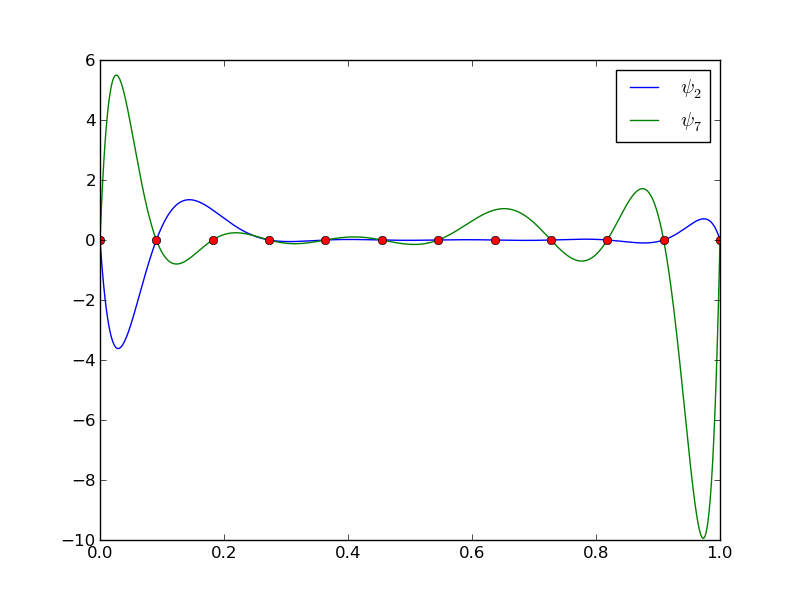
Figure 18
12 punktów, dwa wielomiany stopnia 11 (Uwaga!: \( \psi_2(x_2) \neq 0 \) i \( \psi_7(x_7) \neq 0 \)
Figure 19
Problem: oscylacje w okolicach krańców przedziałów dla większych \( N \).
Odpowiedni dobór węzłów interpolacji – węzły Czebyszewa:
$$ \xno{i} = \half (a+b) + \half(b-a)\cos\left( \frac{2i+1}{2(N+1)}\pi\right),\quad i=0\ldots,N $$na przedziale \( [a,b] \).
Figure 20
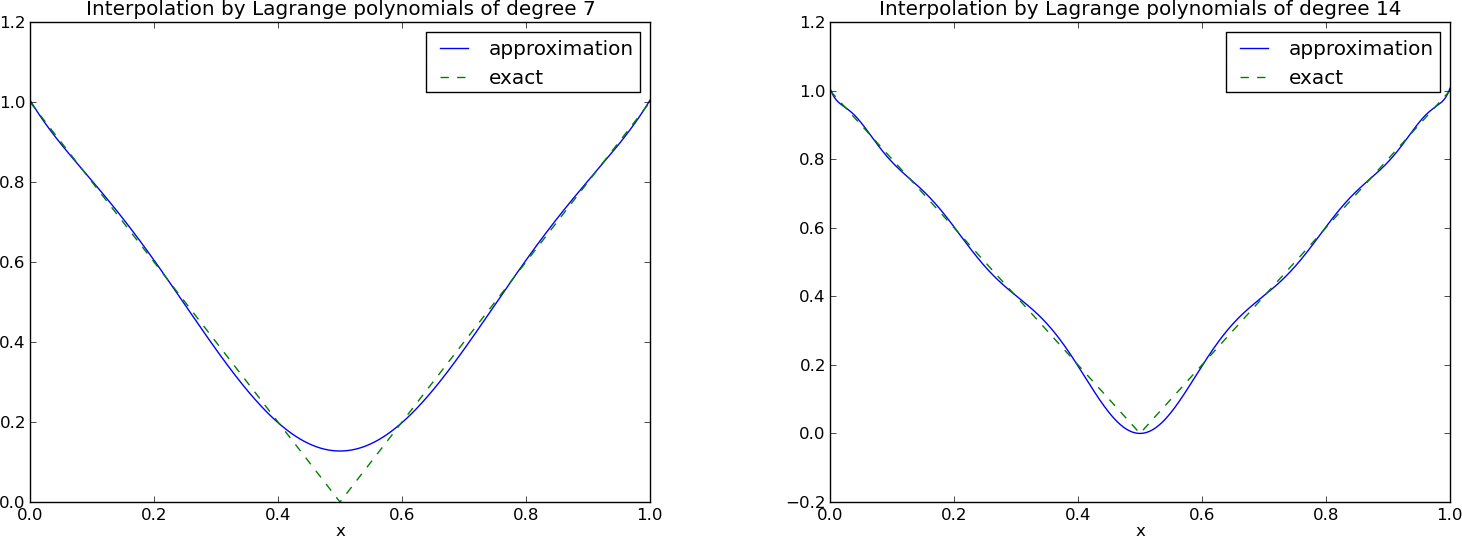
12 punktów, dwa wielomiany stopnia 11.
Uwaga!: Tym razem węzły są inaczej rozmieszczone!
Mniej oscylacyjny charakter wielomianów w porównaniu do węzłów równomiernie rozmieszczonych.
Figure 21
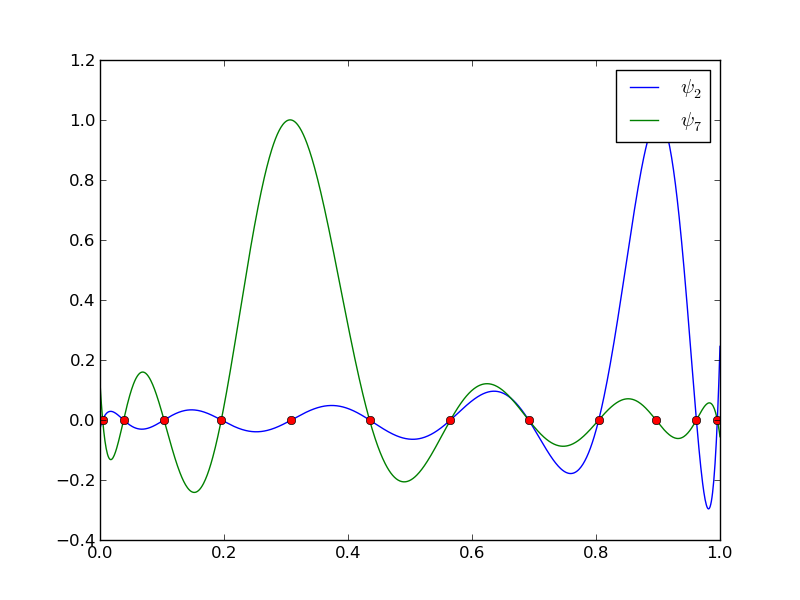
Figure 22
Nośnik funkcji: domknięcie zbioru argumentów funkcji, dla których ma ona wartość różną od zera (takie iksy dla których \( f(x) \neq 0 \))
Figure 23
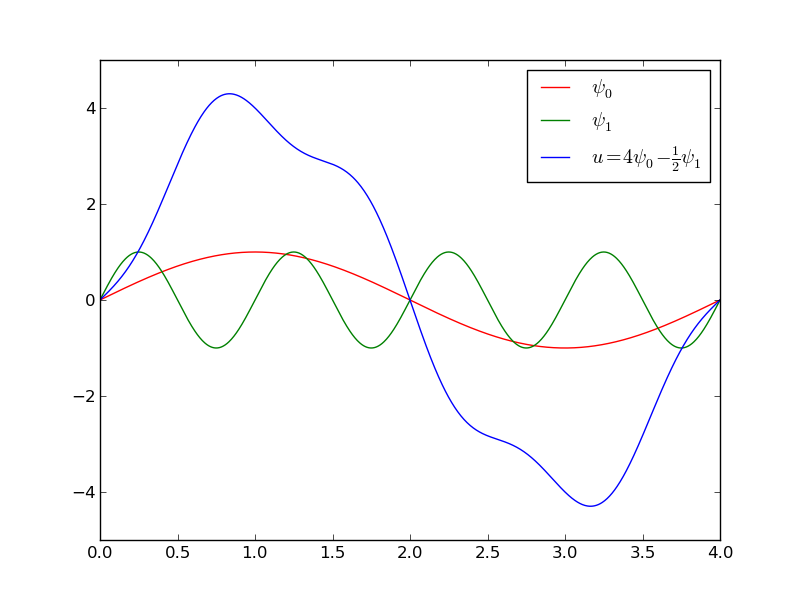
Figure 24

Figure 25
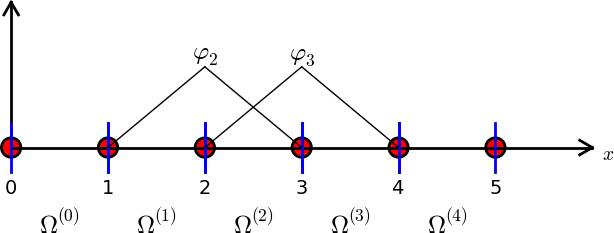
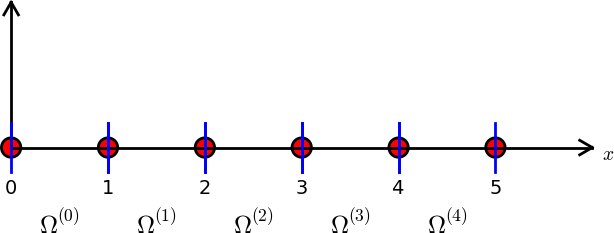
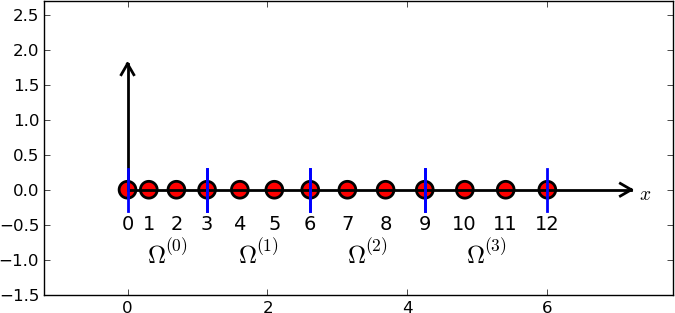
Podzielmy \( \Omega \) na \( N_e \) rozdzielnych podobszarów podobszarów – elementów:
$$ \Omega = \Omega^{(0)}\cup \cdots \cup \Omega^{(N_e)} $$Na każdym elemencie wprowadzamy \( N_n \) wezłów (punktów): \( \xno{0},\ldots,\xno{N_n-1} \)
Figure 26
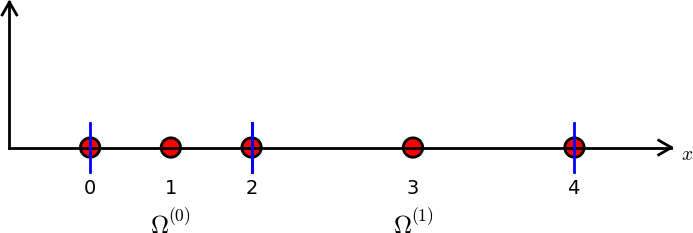
Struktura nodes – współrzędne węzłów.
Struktura elements – numery (globalne) węzłów tworzących
odpowiedni element.
nodes = [0, 1.2, 2.4, 3.6, 4.8, 5]
elements = [[0, 1], [1, 2], [2, 3], [3, 4], [4, 5]]
Figure 27

Figure 28
nodes = [0, 0.125, 0.25, 0.375, 0.5, 0.625, 0.75, 0.875, 1.0]
elements = [[0, 1, 2], [2, 3, 4], [4, 5, 6], [6, 7, 8]]
Figure 29
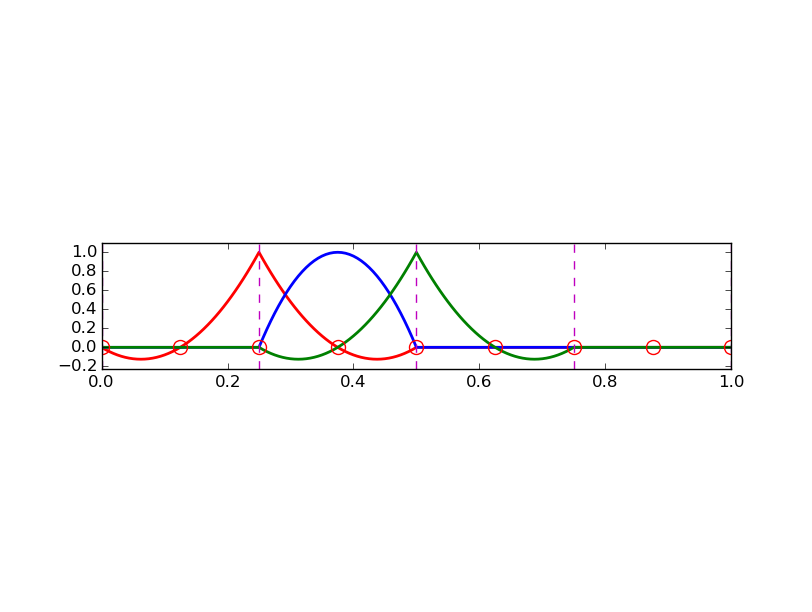
Figure 30
d = 3 # d+1 nodes per element
num_elements = 4
num_nodes = num_elements*d + 1
nodes = [i*0.5 for i in range(num_nodes)]
elements = [[i*d+j for j in range(d+1)] for i in range(num_elements)]
Figure 31
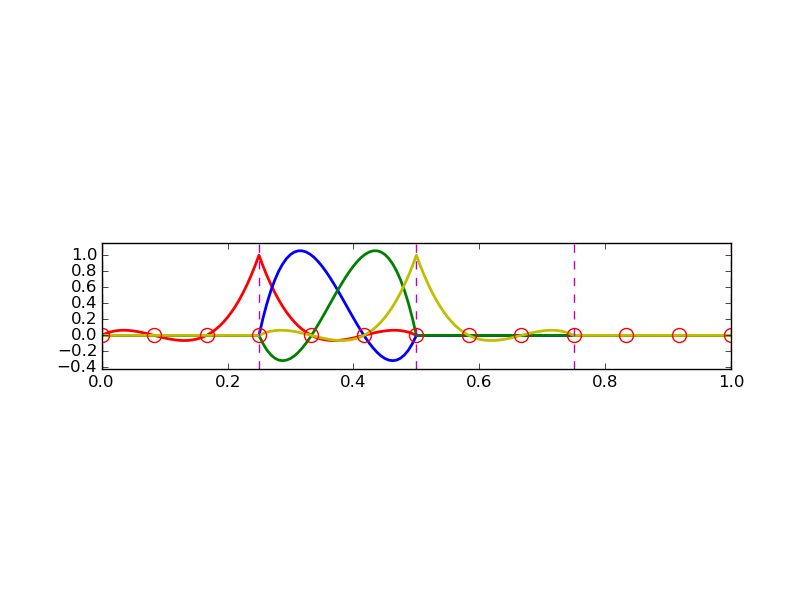
Figure 32
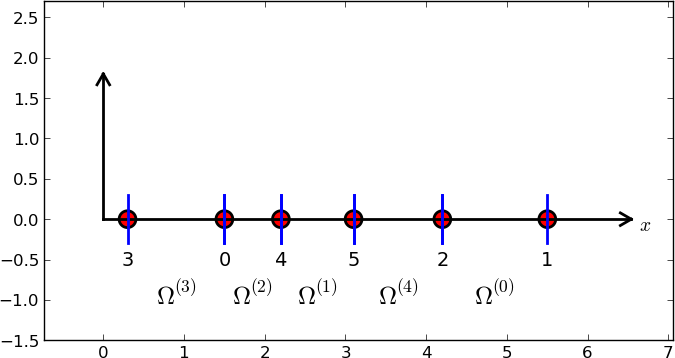
nodes = [1.5, 5.5, 4.2, 0.3, 2.2, 3.1]
elements = [[2, 1], [4, 5], [0, 4], [3, 0], [5, 2]]
Ważna własność: \( c_i \) to wartość funkcji \( u \) w węźle \( i \), \( \xno{i} \):
$$ u(\xno{i}) = \sum_{j\in\If} c_j\basphi_j(\xno{i}) = c_i\basphi_i(\xno{i}) = c_i $$Powód: \( \basphi_j(\xno{i}) =0 \) jeśli \( i\neq j \) i \( \basphi_i(\xno{i}) =1 \)
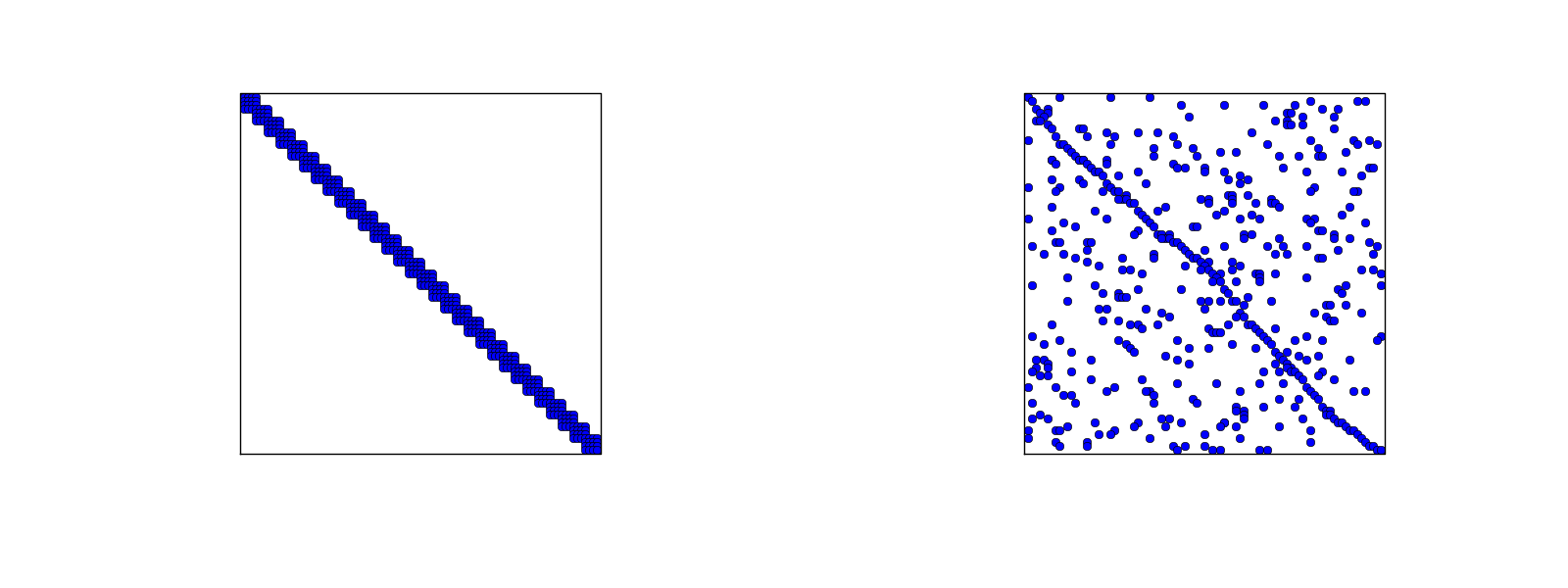
Ponieważ \( A_{i,j}=\int\basphi_i\basphi_j\dx \), większość współczynników macierzy będzie równa zero -> macierze rzadkie
Figure 33
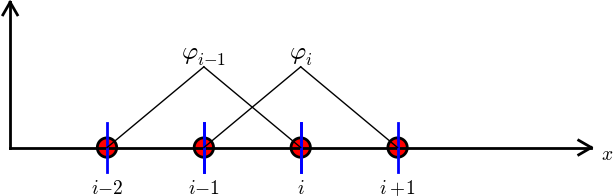
Figure 34

Figure 35
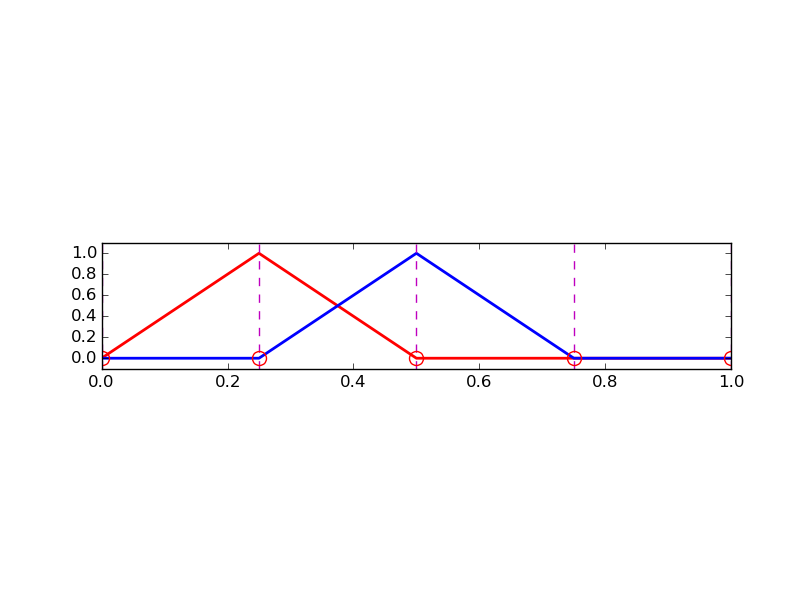
Figure 36

Figure 37

Figure 38

Uproszczenie: elementy jednakowej długości.
\( A_{2,3}=\int_\Omega\basphi_2\basphi_3 dx \): \( \basphi_2\basphi_3\neq 0 \) jedynie na elemencie 2. Dla tego elementu:
$$ \basphi_3(x) = (x-x_2)/h,\quad \basphi_2(x) = 1- (x-x_2)/h$$ $$ A_{2,3} = \int_\Omega \basphi_2\basphi_{3}\dx = \int_{\xno{2}}^{\xno{3}} \left(1 - \frac{x - \xno{2}}{h}\right) \frac{x - x_{2}}{h} \dx = \frac{h}{6} $$Figure 39

Figure 40

Figure 41
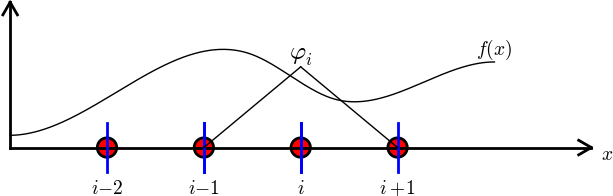
Do dalszych obliczeń potrzebna konkretna postać \( f(x) \) ...
Figure 42

Figure 43
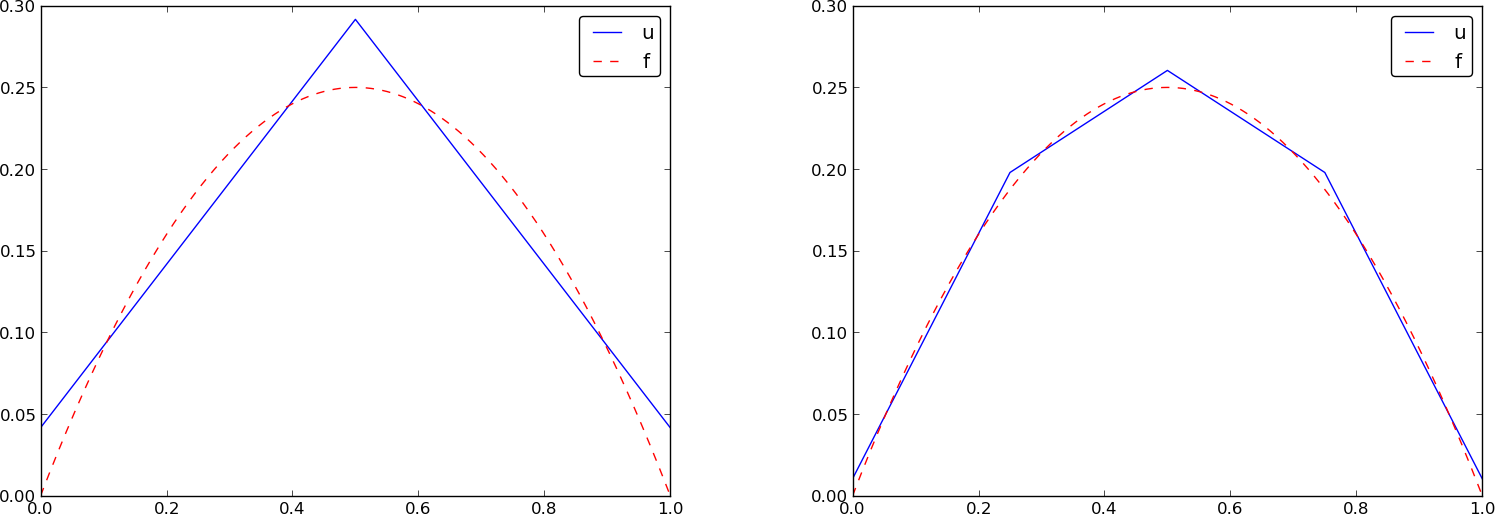
Przypomnienie: jeśli \( f\in V \), \( u \) odtworzy rozwiązanie bezbłędnie. Jeśli \( f \) to parabola, dowolna siatka elementów typu P2 (1 lub wiele elementów) sprawi wygeneruje \( u=f \). To samo dotyczyć będzie elementów typu P3, P4, itd., ponieważ one wszystkie potrafią odtworzyć wielomian 2. stopnia bezbłędnie.
(ang. assemble - gromadzić, składać, zbierać)
assembling, assemblacja?
Figure 44
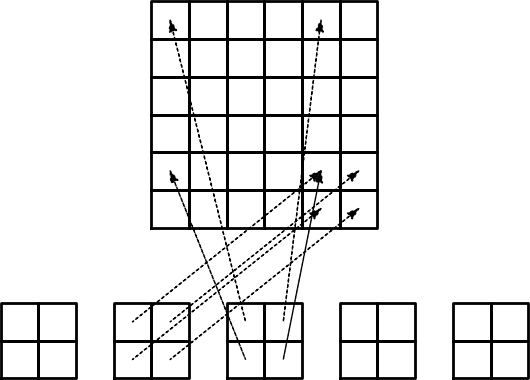
Ważne spostrzeżenia:
Figure 45

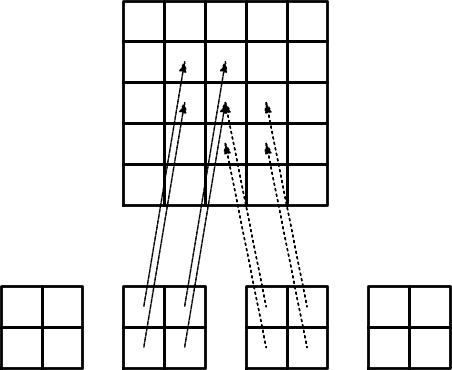
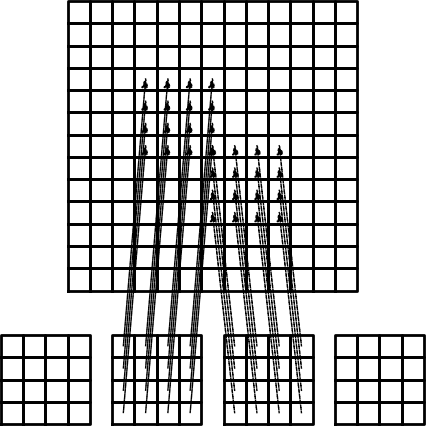
i=elements[e][r]) gdzie: elements = [[1, 2],[2,3],[3,4], ..., [7,8],[8,9,10], ...]| i | e | r |
|---|---|---|
| 1 | 1 | 1 |
| 2 | 1 | 2 |
| 2 | 2 | 1 |
| 3 | 2 | 2 |
| \( \vdots \) | \( \vdots \) | \( \vdots \) |
| 8 | 7 | 2 |
| 8 | 8 | 1 |
| 9 | 8 | 2 |
| 10 | 8 | 3 |
| 10 | 9 | 1 |
| \( \vdots \) | \( \vdots \) | \( \vdots \) |
Figure 46
TODO
Figure 47
TODO
Figure 48

TODO
Figure 49

Ważne spostrzeżenia:
Assembling:
$$ b_{q(e,r)} := b_{q(e,r)} + \tilde b^{(e)}_{r},\quad r\in\Ifd $$Normalizacja współrzędnych położenia:
Zamiast całkować w granicach \( [x_L, x_R] \)
$$ \begin{equation*} \tilde A^{(e)}_{r,s} = \int_{\Omega^{(e)}}\basphi_{q(e,r)}(x)\basphi_{q(e,s)}(x)dx = \int_{x_L}^{x_R}\basphi_{q(e,r)}(x)\basphi_{q(e,s)}(x)dx \end{equation*} $$można transformować przedział \( [x_L, x_R] \) na przedział unormowany \( [-1,1] \) o współrzędnej lokalnej \( X \)
(Transformacja afiniczna)
$$ x = \half (x_L + x_R) + \half (x_R - x_L)X $$inaczej
$$ x = x_m + {\half}hX, \qquad x_m=(x_L+x_R)/2,\quad h=x_R-x_L $$Transformacja odwrotna:
$$ X = \frac{2 x + (x_L + x_R)}{(x_R - x_L)} $$Zmiana granic całkowania -> całkowanie na przedziale unormowanym: podstawienie \( x(X) \) w miejsce \( x \).
Lokalne funkcje bazowe we współrzędnych unormowanych:
$$ \refphi_r(X) = \basphi_{q(e,r)}(x(X)) $$ $$ \begin{array}{c} x = \half (x_L + x_R) + \half (x_R - x_L)X \\ \downarrow \\ dx = \half (x_R - x_L) dX \end{array} $$ $$ \tilde A^{(e)}_{r,s} = \int_{\Omega^{(e)}}\basphi_{q(e,r)}(x)\basphi_{q(e,s)}(x)dx = \int\limits_{-1}^1 \refphi_r(X)\refphi_s(X)\underbrace{\frac{dx}{dX}}_{\det J= h/2}dX $$ $$ \tilde A^{(e)}_{r,s} = \int\limits_{-1}^1 \refphi_r(X)\refphi_s(X)\det J\,dX $$ $$ \tilde b^{(e)}_{r} = \int_{\Omega^{(e)}}f(x)\basphi_{q(e,r)}(x)dx = \int\limits_{-1}^1 f(x(X))\refphi_r(X)\det J\,dX $$(proste funkcje wielomianowe zamiast definicji funkcji na podprzedziałach
Łatwość wygenerowania elementów dowolnego rzędu... Jak?
Założenie: elementy typu P1, oraz funkcja \( f(x)=x(1-x) \).
$$ \begin{align} \tilde A^{(e)}_{0,0} &= \int_{-1}^1 \refphi_0(X)\refphi_0(X)\frac{h}{2} dX\nonumber\\ &=\int_{-1}^1 \half(1-X)\half(1-X) \frac{h}{2} dX = \frac{h}{8}\int_{-1}^1 (1-X)^2 dX = \frac{h}{3} \label{fem:approx:fe:intg:ref:Ae00}\\ \tilde A^{(e)}_{1,0} &= \int_{-1}^1 \refphi_1(X)\refphi_0(X)\frac{h}{2} dX\nonumber\\ &=\int_{-1}^1 \half(1+X)\half(1-X) \frac{h}{2} dX = \frac{h}{8}\int_{-1}^1 (1-X^2) dX = \frac{h}{6} \label{_auto10}\\ \tilde A^{(e)}_{0,1} &= \tilde A^{(e)}_{1,0} \label{fem:approx:fe:intg:ref:Ae10}\\ \tilde A^{(e)}_{1,1} &= \int_{-1}^1 \refphi_1(X)\refphi_1(X)\frac{h}{2} dX\nonumber\\ &=\int_{-1}^1 \half(1+X)\half(1+X) \frac{h}{2} dX = \frac{h}{8}\int_{-1}^1 (1+X)^2 dX = \frac{h}{3} \label{fem:approx:fe:intg:ref:Ae11} \end{align} $$\( x_m \): środek elementu
>>> import sympy as sym
>>> x, x_m, h, X = sym.symbols('x x_m h X')
>>> sym.integrate(h/8*(1-X)**2, (X, -1, 1))
h/3
>>> sym.integrate(h/8*(1+X)*(1-X), (X, -1, 1))
h/6
>>> x = x_m + h/2*X
>>> b_0 = sym.integrate(h/4*x*(1-x)*(1-X), (X, -1, 1))
>>> print b_0
-h**3/24 + h**2*x_m/6 - h**2/12 - h*x_m**2/2 + h*x_m/2
fe_approx1D.pyNiech \( \refphi_r(X) \) będzie wielomianem Lagrange'a stopnia d:
import sympy as sym
import numpy as np
def phi_r(r, X, d):
if isinstance(X, sym.Symbol):
h = sym.Rational(1, d) # node spacing
nodes = [2*i*h - 1 for i in range(d+1)]
else:
# assume X is numeric: use floats for nodes
nodes = np.linspace(-1, 1, d+1)
return Lagrange_polynomial(X, r, nodes)
def Lagrange_polynomial(x, i, points):
p = 1
for k in range(len(points)):
if k != i:
p *= (x - points[k])/(points[i] - points[k])
return p
def basis(d=1):
"""Return the complete basis."""
X = sym.Symbol('X')
phi = [phi_r(r, X, d) for r in range(d+1)]
return phi
def element_matrix(phi, Omega_e, symbolic=True):
n = len(phi)
A_e = sym.zeros((n, n))
X = sym.Symbol('X')
if symbolic:
h = sym.Symbol('h')
else:
h = Omega_e[1] - Omega_e[0]
detJ = h/2 # dx/dX
for r in range(n):
for s in range(r, n):
A_e[r,s] = sym.integrate(phi[r]*phi[s]*detJ, (X, -1, 1))
A_e[s,r] = A_e[r,s]
return A_e
>>> from fe_approx1D import *
>>> phi = basis(d=1)
>>> phi
[1/2 - X/2, 1/2 + X/2]
>>> element_matrix(phi, Omega_e=[0.1, 0.2], symbolic=True)
[h/3, h/6]
[h/6, h/3]
>>> element_matrix(phi, Omega_e=[0.1, 0.2], symbolic=False)
[0.0333333333333333, 0.0166666666666667]
[0.0166666666666667, 0.0333333333333333]
def element_vector(f, phi, Omega_e, symbolic=True):
n = len(phi)
b_e = sym.zeros((n, 1))
# Make f a function of X
X = sym.Symbol('X')
if symbolic:
h = sym.Symbol('h')
else:
h = Omega_e[1] - Omega_e[0]
x = (Omega_e[0] + Omega_e[1])/2 + h/2*X # mapping
f = f.subs('x', x) # substitute mapping formula for x
detJ = h/2 # dx/dX
for r in range(n):
b_e[r] = sym.integrate(f*phi[r]*detJ, (X, -1, 1))
return b_e
Zwróć uwagę na f.subs('x', x) -> podstawienie \( x(X) \) za x w formule na f
(od teraz f jest funkcją \( f(X) \))
sympy zawsze da radęsympy zwróci obiekt typu Integral zamiast liczby)def element_vector(f, phi, Omega_e, symbolic=True):
...
I = sym.integrate(f*phi[r]*detJ, (X, -1, 1)) # try...
if isinstance(I, sym.Integral):
h = Omega_e[1] - Omega_e[0] # Ensure h is numerical
detJ = h/2
integrand = sym.lambdify([X], f*phi[r]*detJ)
I = sym.mpmath.quad(integrand, [-1, 1])
b_e[r] = I
...
def assemble(nodes, elements, phi, f, symbolic=True):
N_n, N_e = len(nodes), len(elements)
zeros = sym.zeros if symbolic else np.zeros
A = zeros((N_n, N_n))
b = zeros((N_n, 1))
for e in range(N_e):
Omega_e = [nodes[elements[e][0]], nodes[elements[e][-1]]]
A_e = element_matrix(phi, Omega_e, symbolic)
b_e = element_vector(f, phi, Omega_e, symbolic)
for r in range(len(elements[e])):
for s in range(len(elements[e])):
A[elements[e][r],elements[e][s]] += A_e[r,s]
b[elements[e][r]] += b_e[r]
return A, b
if symbolic:
c = A.LUsolve(b) # sympy arrays, symbolic Gaussian elim.
else:
c = np.linalg.solve(A, b) # numpy arrays, numerical solve
Uwaga: obliczanie współczynników macierzy A, b oraz rozwiązanie URL
A.LUsolve(b) może być baaardzo czasochłonne$\ldots$
>>> h, x = sym.symbols('h x')
>>> nodes = [0, h, 2*h]
>>> elements = [[0, 1], [1, 2]]
>>> phi = basis(d=1)
>>> f = x*(1-x)
>>> A, b = assemble(nodes, elements, phi, f, symbolic=True)
>>> A
[h/3, h/6, 0]
[h/6, 2*h/3, h/6]
[ 0, h/6, h/3]
>>> b
[ h**2/6 - h**3/12]
[ h**2 - 7*h**3/6]
[5*h**2/6 - 17*h**3/12]
>>> c = A.LUsolve(b)
>>> c
[ h**2/6]
[12*(7*h**2/12 - 35*h**3/72)/(7*h)]
[ 7*(4*h**2/7 - 23*h**3/21)/(2*h)]
>>> nodes = [0, 0.5, 1]
>>> elements = [[0, 1], [1, 2]]
>>> phi = basis(d=1)
>>> x = sym.Symbol('x')
>>> f = x*(1-x)
>>> A, b = assemble(nodes, elements, phi, f, symbolic=False)
>>> A
[ 0.166666666666667, 0.0833333333333333, 0]
[0.0833333333333333, 0.333333333333333, 0.0833333333333333]
[ 0, 0.0833333333333333, 0.166666666666667]
>>> b
[ 0.03125]
[0.104166666666667]
[ 0.03125]
>>> c = A.LUsolve(b)
>>> c
[0.0416666666666666]
[ 0.291666666666667]
[0.0416666666666666]
>>> d=1; N_e=8; Omega=[0,1] # 8 linear elements on [0,1]
>>> phi = basis(d)
>>> f = x*(1-x)
>>> nodes, elements = mesh_symbolic(N_e, d, Omega)
>>> A, b = assemble(nodes, elements, phi, f, symbolic=True)
>>> A
[h/3, h/6, 0, 0, 0, 0, 0, 0, 0]
[h/6, 2*h/3, h/6, 0, 0, 0, 0, 0, 0]
[ 0, h/6, 2*h/3, h/6, 0, 0, 0, 0, 0]
[ 0, 0, h/6, 2*h/3, h/6, 0, 0, 0, 0]
[ 0, 0, 0, h/6, 2*h/3, h/6, 0, 0, 0]
[ 0, 0, 0, 0, h/6, 2*h/3, h/6, 0, 0]
[ 0, 0, 0, 0, 0, h/6, 2*h/3, h/6, 0]
[ 0, 0, 0, 0, 0, 0, h/6, 2*h/3, h/6]
[ 0, 0, 0, 0, 0, 0, 0, h/6, h/3]
Uwaga (zadanie domowe): Wykonaj obliczenia na kartce papieru w celu potwierdzenia wartości poszczególnych elementów powyższej macierzy (pomocne w zrozumieniu materiału).
Figure 50
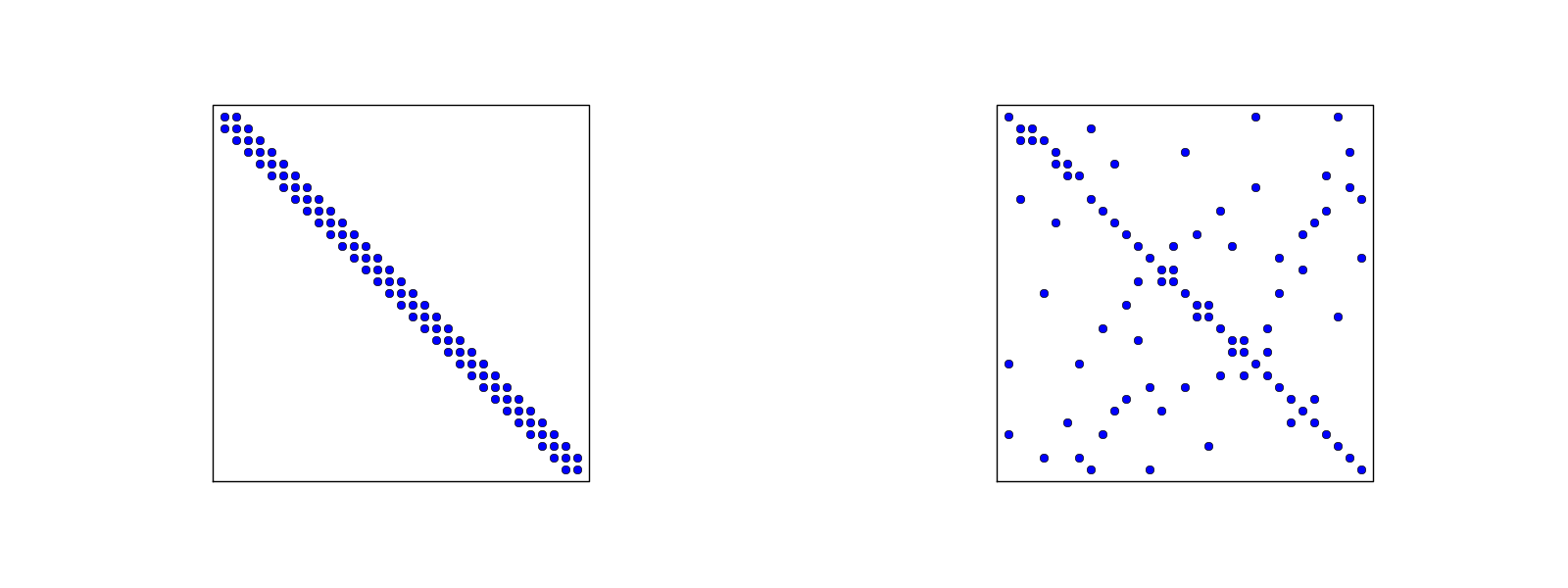
Figure 51
Postać specyficznych macierzy \( A_{i,j} \):
Wskazówki:
scipy.sparseZadanie: Porównać rozwiązanie zadania przybliżenia funkcji \( f(x) \) przy pomocy siatki \( N_e \) elementów skończonych o funkcjach bazowych rzędu \( d \).
import sympy as sym
from fe_approx1D import approximate
x = sym.Symbol('x')
approximate(f=x*(1-x)**8, symbolic=False, d=1, N_e=4)
approximate(f=x*(1-x)**8, symbolic=False, d=2, N_e=2)
approximate(f=x*(1-x)**8, symbolic=False, d=1, N_e=8)
approximate(f=x*(1-x)**8, symbolic=False, d=2, N_e=4)
Figure 52
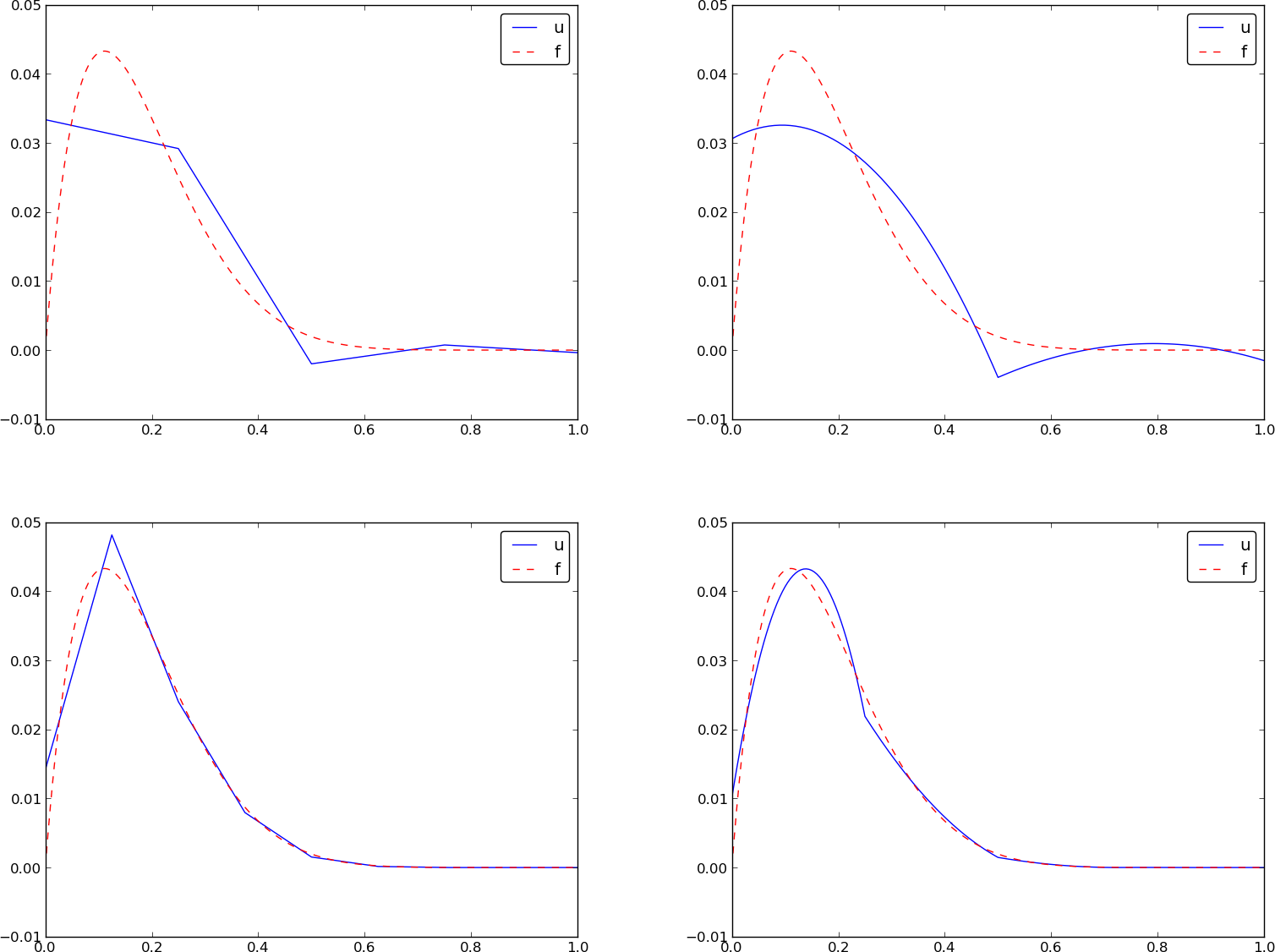
Najczęstsza interpretacja:
wartości \( u \) (wymagane do geometrii i aproksymacji funkcji)
Problem:
– wielkości reprezentowane przez \( c_j \) (niewiadome w URL) -> najczęściej: wartości funkcji w węźle \( \sum_{j\in\If} c_j \basphi_j(\xno{i}) = c_i \)
wierzchołki -> komórki -> interpolacja geometrii
węzły, stopnie swobody -> interpolacja funkcji
vertices, cells, dof_mapvertices (równoważne strukturze nodes dla elementów P1)cells[e][r] numer globalny dla wierchołka r elementu e (równoważne strukturze elements dla elementów typu P1)dof_map[e,r] odwzorowanie lokalnego indeksu stopnia swobody r elementu e na number globalny (równoważne strukturze elements dla elementów typu Pd)W trakcie assemblingu należy skorzystać ze struktury dof_map:
A[dof_map[e][r], dof_map[e][s]] += A_e[r,s]
b[dof_map[e][r]] += b_e[r]
Figure 53

vertices = [0, 0.4, 1]
cells = [[0, 1], [1, 2]]
dof_map = [[0, 1, 2], [2, 3, 4]]
Przykład: Ta sama siatka, ale \( u \) to funkcja stała na każdej komórce (przedziałami stała) -> elementy typu P0.
Te same struktury vertices i cells, ale dodatkowo
dof_map = [[0], [1]]
Można traktować te elementy jak elementy z interpolacją opartą na węźle znajdującym się pośrodku elementu.
Od tej pory będziemy wykorzystywać struktury cells, vertices, i dof_map.
# Use modified fe_approx1D module
from fe_approx1D_numint import *
x = sym.Symbol('x')
f = x*(1 - x)
N_e = 10
# Create mesh with P3 (cubic) elements
vertices, cells, dof_map = mesh_uniform(N_e, d=3, Omega=[0,1])
# Create basis functions on the mesh
phi = [basis(len(dof_map[e])-1) for e in range(N_e)]
# Create linear system and solve it
A, b = assemble(vertices, cells, dof_map, phi, f)
c = np.linalg.solve(A, b)
# Make very fine mesh and sample u(x) on this mesh for plotting
x_u, u = u_glob(c, vertices, cells, dof_map,
resolution_per_element=51)
plot(x_u, u)
Figure 54
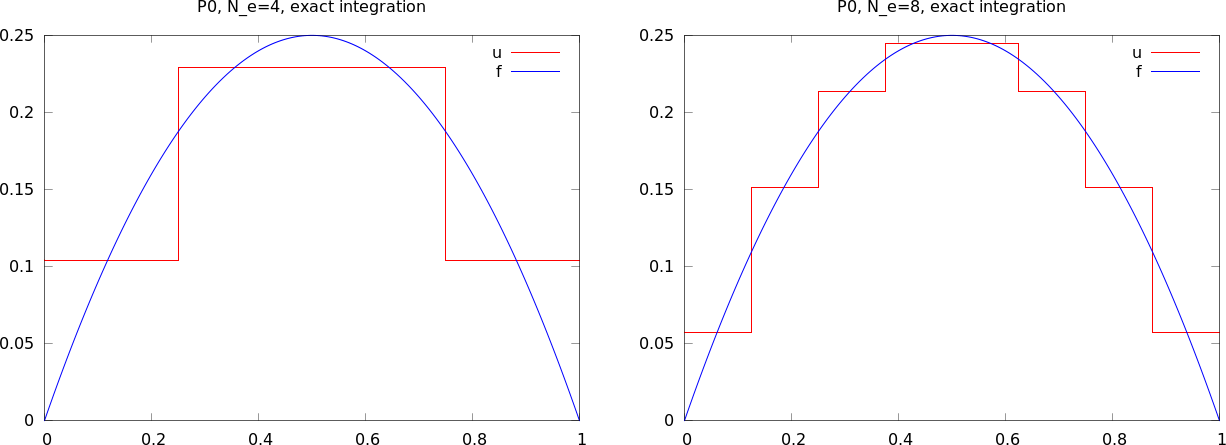
Funkcja approximate ''opakowuje'' polecenia z poprzedniego slajdu:
from fe_approx1D_numint import *
x=sym.Symbol("x")
for N_e in 4, 8:
approximate(x*(1-x), d=0, N_e=N_e, Omega=[0,1])
Błąd jako funkcja:
$$ e(x) = f(x) - u(x) $$Błąd – dyskretna wartość -> normy:
$$ L^2 \hbox{ error: }\quad ||e||_{L^2} = \left(\int_{\Omega} e^2 dx\right)^{1/2}$$Szacowanie całki:
u_glob, które zwróci x i u), a następnie
Ponieważ elementy mogą być różnych rozmiarów (długości) siatka dyskretna może być niejednorodna, (ponadto powtórzone punkty na granicach elementów, widziane z perspektywy dwóch sąsiadujących elementów)
->
potrzebna prymitywna implementacja wzoru trapezów:
$$ \int_\Omega g(x) dx \approx \sum_{j=0}^{n-1} \half(g(x_j) + g(x_{j+1}))(x_{j+1}-x_j)$$# Given c, compute x and u values on a very fine mesh
x, u = u_glob(c, vertices, cells, dof_map,
resolution_per_element=101)
# Compute the error on the very fine mesh
e = f(x) - u
e2 = e**2
# Vectorized Trapezoidal rule
E = np.sqrt(0.5*np.sum((e2[:-1] + e2[1:])*(x[1:] - x[:-1]))
Teoria i eksperymenty pokazują, że aplikacja \( \LSM \) czy metody Galerkina dla elementów skończonych typu Pd o tej samej długości \( h \) daje błąd:
$$ ||e||_{L^2} = C | f^{d+1} | h^{d+1} $$gdzie \( C \) zależy od \( d \) i \( \Omega = [0, L] \) ale nie zależy od \( h \), oraz
$$ |f^{d+1}|^{2} = \int_0^L \left( \frac{d^{d+1}f}{d x^{d+1}} \right)^2 dx $$Niech dana będzie unormowana komórka \( [-1,1] \) z dwoma węzłami \( X=-1 \) i \( X=1 \). Stopnie swobody:
Uwzględnienie wartości pochodnych zadanej funkcji w węzłach jako stopni swobody zapewnia kontrolę ciągłości pochodnej.
4 ogranicznia na \( \refphi_r \) (1 dla stopnia swobody \( r \), 0 dla pozostałych):
Cztery układy równań liniowych z 4 niewiadomymi - współczynnikami wielomianów 3 stopnia.
# definition of the interval ends
x = np.array([-1, 1])
C = [] # list of polynomials stored as coefficients
B = [] # list of basis functions
dB = [] # list of the derivatives of basis functions
for k in np.arange(0,4):
A = np.array( [[ x[0]**3, x[0]**2, x[0], 1 ],
[ 3*x[0]**2, 2*x[0], 1, 0 ],
[ x[1]**3, x[1]**2, x[1], 1 ],
[ 3*x[1]**2, 2*x[1], 1, 0 ]])
b = np.zeros( (4,1) ); b[k] = 1
c = np.linalg.solve(A, b); C.append( c )
B.append( lambda x: C[k][0,0] * x**3 + C[k][1,0] * x**2 + C[k][2,0] * x + C[k][3,0] )
dB.append( lambda x: 3* C[k][0,0] * x**2 + 2*C[k][1,0] * x + C[k][2,0] )
# Check numerically that resulting cubic polynomial
# fulfills imposed requirements
A = [1, 1, 2, 1] # basis function coefficients
# U(x[0]) dU(x[0]) U(x[1]) dU(x[1])
xx = np.arange(-1,1, 0.001)
U = np.zeros(xx.shape)
for k in np.arange(0,4):
U = U + A[k] * B[k](xx)
# numerical approximation of the derivatives at the ends of the interval
dl = (U[1]-U[0])/(xx[1]-xx[0])
dr = (U[-1]-U[-2])/(xx[-1]-xx[-2])
numericalApproximationOfA = [ U[0], dl, U[-1], dr]
print(numericalApproximationOfA)
Wynik działania skryptu:
[1.0, 0.9992502500000269, 1.999000749750002, 0.9977517500000526]
Figure 55
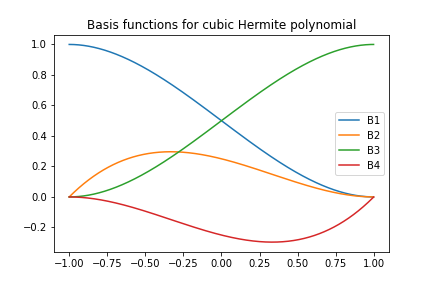
Figure 56
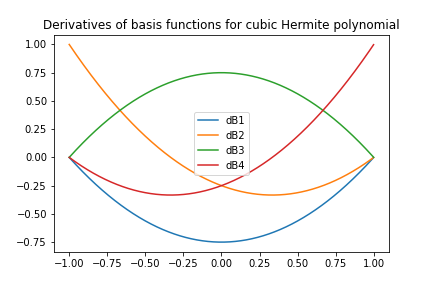
Figure 57
gdzie
Różne metody -> różny wybór węzłów i wag
(ang. midpoint rule) – metoda punktu środkowego
Najprostsza metoda
$$ \int_{-1}^{1} g(X)dX \approx 2g(0),\quad \bar X_0=0,\ w_0=2, $$Dokładna dla funkcji podcałkowych będących wielomianami 1. stopnia
Wzór trapezów:
$$ \int_{-1}^{1} g(X)dX \approx g(-1) + g(1),\quad \bar X_0=-1,\ \bar X_1=1,\ w_0=w_1=1, $$Wzór Simpsona (parabol):
$$ \int_{-1}^{1} g(X)dX \approx \frac{1}{3}\left(g(-1) + 4g(0) + g(1)\right), $$gdzie
$$ \bar X_0=-1,\ \bar X_1=0,\ \bar X_2=1,\ w_0=w_2=\frac{1}{3},\ w_1=\frac{4}{3} $$Plik `numint.py zawiera zbiór węzłów i wag dla metody Gaussa-Legendre'a.
Rozwiązania i algorytmy przedstawione dla aproksymacji funkcji \( f(x) \) w 1D da się rozwinąć i ''przenieść'' na przypadki funkcji \( f(x,y) \) w 2D i \( f(x,y,z) \) w 3D. Ogólne wzory pozostają takie same.
Iloczyn skalarny w 2D:
$$ (f,g) = \int_\Omega f(x,y)g(x,y) dx dy $$Zastosowanie \( \LSM \) lub metody Galerkina da URL:
$$ \begin{align*} \sum_{j\in\If} A_{i,j}c_j &= b_i,\quad i\in\If\\ A_{i,j} &= (\baspsi_i,\baspsi_j)\\ b_i &= (f,\baspsi_i) \end{align*} $$Problem: Jak skonstruować dwuwymiarowe funkcje bazowe \( \baspsi_i(x,y) \)?
Korzystając z funkcji bazowych 1D zmiennej \( x \) oraz funkcji bazowych 1D zmiennej \( y \):
$$ \begin{align} V_x &= \mbox{span}\{ \hat\baspsi_0(x),\ldots,\hat\baspsi_{N_x}(x)\} \label{fem:approx:2D:Vx}\\ V_y &= \mbox{span}\{ \hat\baspsi_0(y),\ldots,\hat\baspsi_{N_y}(y)\} \label{fem:approx:2D:Vy} \end{align} $$Przestrzeń wektorowa 2D może być zdefinowana jako iloczyn tensorowy \( V = V_x\otimes V_y \) z funkcjami bazowymi:
$$ \baspsi_{p,q}(x,y) = \hat\baspsi_p(x)\hat\baspsi_q(y) \quad p\in\Ix,q\in\Iy\tp $$Niech dane będą dwa wektory \( a=(a_0,\ldots,a_M) \) i \( b=(b_0,\ldots,b_N) \). Ich zewnętrznym iloczynem tensorowym ( iloczynem diadycznym jeśli \( N=M \)) jest \( p=a\otimes b \) zdefiniowane jako:
$$ p_{i,j}=a_ib_j,\quad i=0,\ldots,M,\ j=0,\ldots,N\tp$$Uwaga: \( p \) to macierz/tablica dwuwymiarowa
Przykład: baza 2D jako iloczyn tensorowy przestrzeni 1D:
$$ \baspsi_{p,q}(x,y) = \hat\baspsi_p(x)\hat\baspsi_q(y), \quad p\in\Ix,q\in\Iy$$ iloczyn tensorowy macierzy(dowolnych wymiarów) ->
iloczyn tensorowy wektorów(dowolnych wymiarów) ->
iloczyn diadyczny(tego samego wymiaru)
tensorBaza przestrzeni 2D wymaga dwóch indeksów (i podwójnego sumowania) :
$$ u = \sum_{p\in\Ix}\sum_{q\in\Iy} c_{p,q}\baspsi_{p,q}(x,y) $$Lub tylko jednego indeksu
$$ u = \sum_{j\in\If} c_j\baspsi_j(x,y)$$jeśli posiadamy odwzorowanie \( (p,q)\rightarrow i \):
$$ \baspsi_i(x,y) = \hat\baspsi_p(x)\hat\baspsi_q(y), \quad i=p (N_y+1) + q\hbox{ or } i=q (N_x+1) + p $$Dla dwuelementowej bazy 1D
$$ \{ 1, x \} $$iloczyn tensorowy (wszystkie kombinacje) generuje bazę przestrzeni 2D:
$$ \baspsi_{0,0}=1,\quad \baspsi_{1,0}=x, \quad \baspsi_{0,1}=y, \quad \baspsi_{1,1}=xy $$W notacji jednoindeksowej:
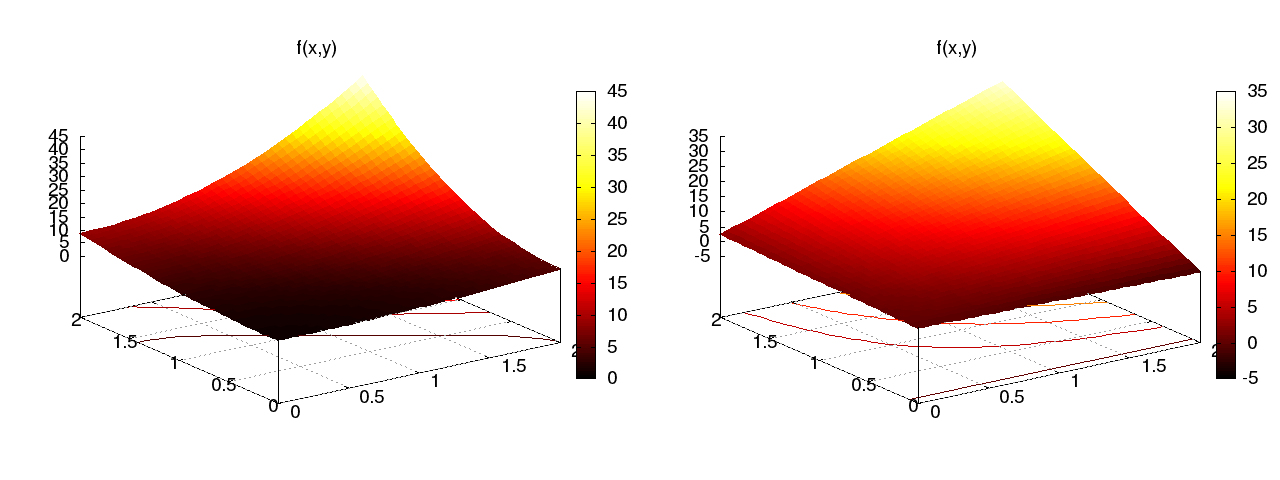
$$ \baspsi_0=1,\quad \baspsi_1=x, \quad \baspsi_2=y,\quad\baspsi_3 =xy $$Funkcja aproksymowana (kwadratowa) \( f(x,y) = (1+x^2)(1+2y^2) \) (po lewej), funkcja aproksymująca (biliniowa) \( u \) (po prawej) (\( x^2y^2 \) vs \( xy \)):
Figure 58
Zmiany w kodzie w stosunku do wersji 1D (approx1D.py):
Omega = [[0, L_x], [0, L_y]]import sympy as sym
integrand = psi[i]*psi[j]
I = sym.integrate(integrand,
(x, Omega[0][0], Omega[0][1]),
(y, Omega[1][0], Omega[1][1]))
# Fall back on numerical integration if symbolic integration
# was unsuccessful
if isinstance(I, sym.Integral):
integrand = sym.lambdify([x,y], integrand)
I = sym.mpmath.quad(integrand,
[Omega[0][0], Omega[0][1]],
[Omega[1][0], Omega[1][1]])
Iloczyn tensorowy bazy potęgowej \( x^i \) (bazy Taylora):
def taylor(x, y, Nx, Ny):
return [x**i*y**j for i in range(Nx+1) for j in range(Ny+1)]
Iloczyn tensorowy bazy sinusoidalnej \( \sin((i+1)\pi x) \):
def sines(x, y, Nx, Ny):
return [sym.sin(sym.pi*(i+1)*x)*sym.sin(sym.pi*(j+1)*y)
for i in range(Nx+1) for j in range(Ny+1)]
Cały kod w approx2D.py.
>>> from approx2D import *
>>> f = (1+x**2)*(1+2*y**2)
>>> psi = taylor(x, y, 1, 1)
>>> Omega = [[0, 2], [0, 2]]
>>> u, c = least_squares(f, psi, Omega)
>>> print u
8*x*y - 2*x/3 + 4*y/3 - 1/9
>>> print sym.expand(f)
2*x**2*y**2 + x**2 + 2*y**2 + 1
Dodajemy funkcje bazowe o wyższych potęgach tak, aby \( f\in V \). Spodziewany wynik: \( u=f \)
>>> psi = taylor(x, y, 2, 2)
>>> u, c = least_squares(f, psi, Omega)
>>> print u
2*x**2*y**2 + x**2 + 2*y**2 + 1
>>> print u-f
0
Kluczowa idea:
$$ V = V_x\otimes V_y\otimes V_z$$$$ \begin{align*} a^{(q)} &= (a^{(q)}_0,\ldots,a^{(q)}_{N_q}),\quad q=0,\ldots,m\\ p &= a^{(0)}\otimes\cdots\otimes a^{(m)}\\ p_{i_0,i_1,\ldots,i_m} &= a^{(0)}_{i_1}a^{(1)}_{i_1}\cdots a^{(m)}_{i_m} \end{align*} $$
W szczególności dla 3D:
$$ \begin{align*} \baspsi_{p,q,r}(x,y,z) &= \hat\baspsi_p(x)\hat\baspsi_q(y)\hat\baspsi_r(z)\\ u(x,y,z) &= \sum_{p\in\Ix}\sum_{q\in\Iy}\sum_{r\in\Iz} c_{p,q,r} \baspsi_{p,q,r}(x,y,z) \end{align*} $$Zalety \( \FEM \) w zastosowaniach 2D i 3D:
\( \FEM \) w 1D: głównie dla celów dydaktycznych, debugowania
2D:
3D:
Figure 59
Figure 60
Figure 61
Element trójkątny typu P1: aproksymacja \( u \) na każdym elemencie (komórce) funkcją liniową \( ax + by + c \)
Figure 62
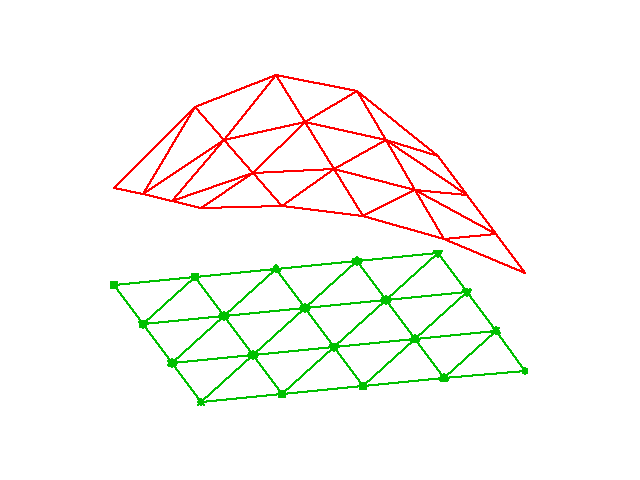
Figure 63

Figure 64
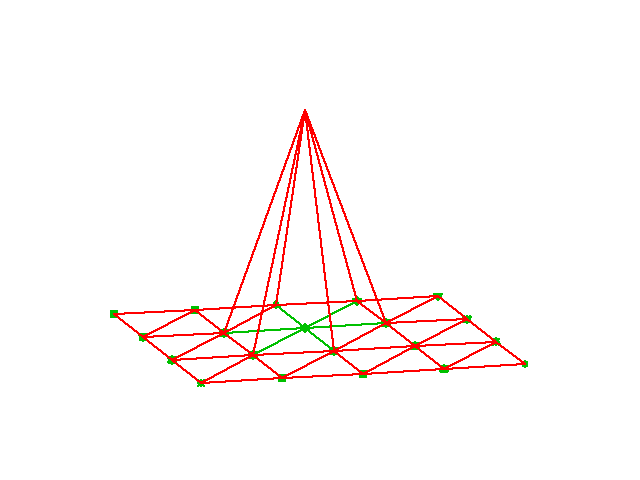
Figure 65

Funkcje bazowe \( \refphi_r \) wyższych stopni opierają się na większej liczbie węzłów (stopni swobody)
Figure 66

Figure 67

Figure 68

Transformacja (Odwzorowanie) komórki we współrzędnych unormowanych
\( \X = (X,Y) \)do komórki we współrzędnych globalnych:
\( \x = (x,y) \): $$ \begin{equation} \x = \sum_{r} \refphi_r^{(1)}(\X)\xdno{q(e,r)} \label{fem:approx:fe:affine:map} \end{equation} $$gdzie
Odwzorowanie zachowuje liniowość ścian i krawędzi.
Figure 69

Idea: Wykorzystanie funkcji bazowych elementu (nie tylko funkcji typu P1 ale i wyższych rzędów) do odwzorowania geometrii:
$$ \x = \sum_{r} \refphi_r(\X)\xdno{q(e,r)} $$Zaleta: pozwala generować elementy o geomtrii nielinowej
Figure 70

Wymagana transformacja całek z \( \Omega^{(e)} \) (komórka we współrządnych globalnych) w \( \tilde\Omega^r \) (komórka unormowana/odniesienia):
$$ \begin{align} \int_{\Omega^{(e)}}\basphi_i (\x) \basphi_j (\x) \dx &= \int_{\tilde\Omega^r} \refphi_i (\X) \refphi_j (\X) \det J\, \dX \label{_auto22}\\ \int_{\Omega^{(e)}}\basphi_i (\x) f(\x) \dx &= \int_{\tilde\Omega^r} \refphi_i (\X) f(\x(\X)) \det J\, \dX \label{_auto23} \end{align} $$gdzie \( \dx = dx dy \) lub \( \dx = dxdydz \) oraz \( \det J \) to wyznacznik jakobianu odwzorowania \( \x(\X) \).
$$ J = \left[\begin{array}{cc} \frac{\partial x}{\partial X} & \frac{\partial x}{\partial Y}\\ \frac{\partial y}{\partial X} & \frac{\partial y}{\partial Y} \end{array}\right], \quad \det J = \frac{\partial x}{\partial X}\frac{\partial y}{\partial Y} - \frac{\partial x}{\partial Y}\frac{\partial y}{\partial X} $$Odwzorowanie afiniczne \eqref{fem:approx:fe:affine:map}: \( \det J=2\Delta \), \( \Delta = \hbox{powierzchnia komórki/elementu} \)
Ogólna idea \( \FEM \) oraz kroki algorytmu – takie same niezależnie od wymiarowości geometrii.
Im wyższy wymiar przestrzeni, tym większy nakład obliczeniowy. ze względu na komplikację wzorów.
Obliczenia ręczne - nużące, podatne na popełnienie pomyłki.
Automatyzacja i algorytmizacja problemu pożądana.